Análisis Matemático - Límites

Contenido

Apunte de Límites: Conjuntos. Funciones. Superficie de nivel. Parametrizaciones. Curvas en R3.

ANALISIS II

Conjuntos:

Abierto: Es aquel que no incluye la frontera (todos los puntos son interiores).

Cerrado: Es aquel que incluye toda su frontera.

Acotado: R es acotado si $k > 0 / R Ì E (0, k)

Compacto: cerrado y acotado.

Conexo: Cuando dados 2 puntos cualesquiera del conjunto, se los puede unir con una curva que este incluida en el conjunto.

Convexo: Cuando dados 2 puntos cualesquiera del conjunto, el segmento que los une esta incluido en el conjunto.

Si es convexo:

No es convexo:

Funciones:

F: A Ì R^m ® , m > 1 campo vectorial

F: A Ì Rⁿ ® R, m = 1 campos o funciones escalares

Conjunto de nivel (para campos escalares):

Definición: dada F: A Ì Rⁿ ® R y k Ì R, se llama conjunto de nivel k de F al conjunto de puntos de A tal que F (x) = k

Para f: A Ì R ² ® R: F (x, y) = k = > curva de nivel

Para f: A Ì R³ ® R: F (x, y, z) = k = > superficie de nivel

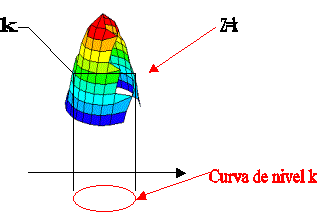
Interpretación geométrica: El conjunto de nivel k de una función de 2 variables x e y es la sombra o la proyección de la curva que resulta de intersectar el grafico de la función con el plano z = k.

Superficie de nivel:

F (x, y, z) = k

Ejemplos:

1) 3x-2y + z = k	para k = 1	3x-2y + z = 1		(x, y, z) (3, -2, 1) = k		fijo
	para k = -2	3x-2y + z = -2		(x-a). v = 0 Þx. v = a. v	Þ

ÞSi varío k, varío el origen del plano (lo desplazo)

A medida que vario k me van quedando planos paralelos.

Ejemplos:

F (x, y) = y-2x, x Ì R ²

Planteo F (x, y) = k, k Ì R Þ y-2x = k Þy = 2x + k

F (x, y, z) = z-x ²-y ²-4

Planteo F (x, y, z) = k Þz-x ²-y ²-4 = k Þ z = x ² + y ² + 4 + k

Parametrizaciones: Curvas en R ²

a)F (x) = x ², x Ì [-1, 4]

- Ecuación cartesiana del grafico de F:	y = F (x) = > Y = x ², -1 ≤x ≤ 4
- Ecuación vectorial del grafico de F	x = (t, t ²), t Ì [-1, 4]
- Ecuaciones paramétricas del grafico de F	x = t y = t ², t Ì [-1, 4]

La función g: [-1, 4] ® R ² se denomina parametrización del grafico de F y esta definida por: g (t) = (t, t ²), t Ì [-1, 4]

b)F (x) = 2x + 1, x Ì R Ec cartesiana y = 2x + 1, x Ì R.

Parametrización: intento x = t Þy = 2t + 1 } g (t) = (t, 2t + 1), t Ì R

X = (t, 2t + a), t Ì R Ec vectorial.

Parametrización de una circunferencia:

x ² + y ² = R ²	EP x = R cos (t), t Ì [0, 2 π ]
	y = R sen (t)
	EV x = (R cos (t), R sen (t)), t Ì [0, 2 π ]
	G = (R cos (t), R sen (t)), t Ì [0, 2 π ]

Obs: Para recorrer las curvas de manera inversa a la normal: de [a, b] pasa a [-b, -a]

Curva: Definición: Dada una función g: [a, b]Ì R ® Rⁿ, continua, se llama curva al conjunto imagen de g

Curva no completa = arco de curva.

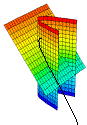
Curvas en R³

Z + y = 3	EP =	x = t
Y = x ²		y = t ²	EVG (t) = (t, t ², 3-t ²), t Ì R
	Z = 3-t ²

Superficie: Definición: Dada una función g: A Ì R ² ® Rⁿ, continua, se llama superficie al conjunto imagen de g

Limites: Propiedades:

6) si F(x) = b Ù g(y) = L Þ (g o F)(x) = L

7) si F(x) = L Û F_i(x) = L_i, 1 ≤ i ≤ m; (se acercan las componentes).

Limites por curvas: Si no $el lim para alguna curva parametrizada por g tal que g (t₀) = A Þno $ F(x)

Ejemplo: (x - y - 2)/(x - 1)

Tomo y = 1 Þ (x - 1)/(x - 1) = 1

Tomo x = 1 Þ (y - 1)/(1 - y) = -1

Luego, no existe F(x,y) = 1

Obs: La curva que propongo, debe pasar por el punto de trabajo del limite.

Recordar: |x| ≤ |x| Þ x ² ≤ x ² + y ² Þ x ²/(x ² + y ²) ≤ 1

Continuidad:

5) F continua en x₀ yG continua en F (x₀) Þ(G₀F) continua en x₀.

6) F continua en x₀ < = > F_i continua en x₀, 1≤i ≤ m

Tipos de discontinuidad:

1) Esencial: cuando no existe F(x)

2) Evitable: cuando existe el lim pero no F (x₀) o bien $F (x₀) pero lim ≠ F (x₀)

Derivabilidad: Definición: derivada direccional: dada F: A Ì Rⁿ ® R^m, x₀ y ř Ì Rⁿ, se define la derivada direccional de F en x₀ según el versor ř como:

F´(x₀,γ) = [F(x₀ + h.γ) - F(x₀)]/h = ∂F(x₀)/∂γ

Propiedades: principio de homogeneidad: F ´ (x₀, λ ř) = λ F ´ (x₀, ř), λ ≠ 0, λ Ì R

Propiedad 2: Si existe la derivada direccional en un punto, existen las derivadas de las componentes y viceversa.

Derivadas parciales: caso especial de direccionales. Una derivada parcial es una direccional respecto de un versor de la base canónica.

Regla practica de calculo:

1) F (x, y) = ln (x ² + y ²)

F´_x(x, y) = 2.x/(x ² + y ²)

F´_y(x, y) = 2.y/(x ² + y ²)

Dom (F´_x) I Dom (F)

Observación: La derivada de un vector es la derivada de las componentes.

Interpretación geométrica:

Válida para F: A Ì R ² ® R

F´(x₀,y₀) = [F(x₀ + h,y₀) - F(x₀,y₀)]/h = tg α

Teorema del valor medio:

a) dada F: [a, b] ® R, continua en [a, b] y derivable en (a, b), entonces existe c Ì (a, b) tal que:

F (b)-F (a) = F´ (c). (b-a)

b) Dada F: A Ì Rⁿ ® R, A abierto y convexo, F Ì C¹, a Ì A y b Ì A, entonces:

F (b) - F (a) = F ´ (c, b-a) = F ´ (c, ř) |b-a|, γ = (b - a)/|b - a|, c Ì segmento a b,

c ≠ a y c ≠ b

Aplicaciones a curvas: Definición: Punto regular: Dada C curva de Rⁿ, de ecuación vectorial x = g (t) t Ì A, se dice que A Ì C, A = g (t₀), es un punto regular de C si : a)$g ´ (t₀) y b) g ´ (t₀) ≠ 0

Observaciones:

a) si un punto no es regular se lo llama singular.

b) Si una curva tiene todos los puntos regulares Þes regular.

Vector tangente

Definición: Dada C c Rⁿ (C curva de Rⁿ) una curva regular, entonces el vector g ´ (t₀) es tangente a la curva en el punto g (t₀) siendo x =g (t), t Ì A, la ecuación vectorial de la curva, y t₀ Ì A.

F´(t₀) = [F´_x(t₀ + h) - F´_x(t₀)]/h (estamos con una sola variable)

Recta tangente

La curva se confunde con la recta tangente en el punto dado. En R ² y en R³: x = λ g ´ + g (t₀), λ Ì R

Plano normal en R³

Ec vectorial g ´ (t₀). (x-g (t₀)) = 0

G1´ (t₀) (x-g1 (t₀)) + g2´ (t₀) (y-g2 (t₀)) + g3´ (t₀) (z-g3 (t₀)) = 0

Gradiente: se define solo para campos escalares, F A Ì Rⁿ ® R

Grad(F)(x₀) = ÑF(x₀) =[∂F(x₀)/∂x₁, ∂F(x₀)/∂x₂, ... , ∂F(x₀)/∂x_n,]

Dom (ÑF) = dom (F ´ _x1) ∩ dom (F ´ _x2) ∩. . . dom (F ´ _xn) Ì dom (F)

ÑF: B Ì Rⁿ ® Rⁿ

Derivadas de orden superior (parciales)

Definiciones: dada F: A Ì R ² ® R, F Ì C ² (clase 2), se define:

F"(x₀,y₀) = = [F´_x(x₀ + h,y₀) - F´_x(x₀,y₀)]/h

Las derivadas que tienen las mismas letras son iguales: F"´ _xxy = F"´ _xyx = F"´ _yxx

Dominios: Dom (F´ _x) Ì Dom (F)

Dom (F´ _y) Ì Dom (F)

Dom (F" _yx) Ì Dom (F´_x) Ì Dom (F)

Dom (F" _yx) Ì Dom (F´_y) Ì Dom (F)

Teorema de Schwartz

Dada F: A Ì Rⁿ ® R, x₀ Ì A, entonces si$ F" _xy (x) " x Ì E (x₀) y F" _yx (x)" x Ì E (x₀) y F" _xy continua en E (x₀) y F" _yx continua en E (x₀), debe ser F" _xy (x₀) = F" _yx (x₀)

Generalmente pasa para funciones continuas

Extensión a mayor orden

Tomo F: A Ì Rⁿ ® R, suponemos derivadas parciales de cualquier orden continuas.

Entonces: a) Por el teorema de Schwartz Þ F" _xy = F" _yx

Luego F"´ _xyx = F"´ _yxx, por ser la derivada de la misma función.

b)Tomamos F´_x, por teorema de Schwartz F"´ _xxy = F"´ _xyx

c)Finalmente, por a y b resulta: F"´ _xxy = F"´ _xyx = F"´ _yxx

Ejemplo:

1)

F (x, y) = e xy F" xx = y ².e xy F"´ xxy = 2.y.e xy + y ².x.e xy

F´x = y.e xy F" yy = x ² .e xy F"´ xyx = 2.y.e xy + y ².x.e xy

F´y = x.e xy F" xy = e xy + y.x.e xy F"´ yxx = 2.y.e xy + y ².x.e xy

- F" yx = e xy + x.y.e xy -

Diferenciabilidad:

Definición: Dada F: A Ì Rⁿ ® Rⁿ, x₀ Ì A, A abierto, se dice que F es diferenciable en x₀ si $ D (x₀)Ì
R ^mxn tal que:

[F(x) - F(x₀) - dF(x₀).(x - x₀)]/|x - x₀| = 0

F´ ((a, b), ř) = ÑF (a, b).ř (Si F es diferenciable)

Propiedades:

F es F, G es G y x₀ es x₀

1)F y G diferenciables en x₀ Þ F + G diferenciables en x₀

2) F diferenciable en x₀ Þ λ F diferenciable en x₀

3) F y G diferenciables en x₀ Þ FG diferenciable en x₀

4)F diferenciable en x₀ y F (x₀) ≠ 0 Þ 1/F diferenciable en x₀

5)F diferenciable en x₀ y g diferenciable en F (x₀) Þ g_oF diferenciable en x₀

6)F diferenciable en x₀ < = > F_i diferenciable en x₀, 1≤ i ≤ m

Teorema: Dada F: A Ì Rⁿ ® R^m, A abierto, x₀Ì A, tal que F es diferenciable en x₀, entonces F es continua en x₀.

Corolario: Si F no es continua en x₀ = > F no es diferenciable en x₀

Teorema: Dada F: A Ì Rⁿ ® R^m, A abierto, x₀Ì A, tal que F es diferenciable en x₀, entonces $ F´ (x₀, ř)," ř Ì Rⁿ. (Existe la derivada en cualquier dirección).

Corolario:

1) Si para algún ř Ì Rⁿ no$ F´ (x₀, ř) Þ F no es diferenciable en x₀.

2) Si para algún ř Ì Rⁿ $ F´ (x₀, ř) pero F´ (x₀, ř) ≠ dF (x₀) ř Þ F no es diferenciable en x₀.

La matriz dF (x₀) es la matriz de las derivadas parciales de F en x₀. Se llama matriz Jacobiano.

Ejemplo:

1) F (x, y) = (xy ², x ²e^y)

dF =	y ²	2.x.y	=	1	2
	2.x.ey	x ².ey		3	4

Siendo:

1 la derivada con respecto a x de xy ²

2 la derivada con respecto a y de xy ²

3 la derivada con respecto a x de x ²e^y

4 la derivada con respecto a y de x ²e^y

2)

Plano tangente al grafico de F en el punto (x₀, y₀, F (x₀, y₀))

Zt = F (x₀) + F´ (x₀) (x-x₀) + F´y (x₀) (y-y₀) Luego: F (x) @ Zt, x Ì E (x₀)

Análisis de Continuidad

(x ².y)/(x ² + y ²) = y.[x ²/(x ² + y ²)] = 0; x ²≤ x ² + y ² ® hace acotada

Análisis de Derivabilidad

Aplicación a superficies

Superficie: Definición: Dada G, A Ì R ² ® R³, continua, se llama superficie al conjunto imagen de G. Dicha superficie tendrá la ecuación vectorial x = G (u; w); (u; w) Ì A

Clasificación de funciones:

1)F Ì C° (o es de clase C°) continua

2)F Ì C¹ (o es de clase C¹): tiene derivadas parciales continuas.

3)F Ì C ² (o es de clase C ²): tiene derivadas parciales de segundo orden continuas.

∞)F Ì C^∞ (o es de clase C^∞): tiene derivadas parciales de todo orden continuas.

Propiedad: Si F es de una clase también es de todas las clases inferiores.

Teorema: Dada F: A Ì Rⁿ ® R^m, A abierto, tal que FÌ C¹ en E (x₀) Þ F es diferenciable en x₀

Punto regular:

Dado S Ì R³ una superficie de ecuación vectorial x = G (u; w), se dice que el punto x₀ = G (u0; w0) Ì S es regular si: a) $ G´_u (u0; w0) y$ G´_w (u0; w0)

b) G´_u (u0; w0) x G´_w (u0; w0) ≠ 0 (No paralelos)

Si todos los puntos de una S son regulares, es una superficie regular, si además los G´_u y G´_w no colinan es una S lisa o suave.

Teorema: Dada A Ì R ² ® R, A abierto, F es diferenciable en x₀Ì A Þ el grafico de F es una superficie regular en el punto (x₀, y₀, F (x₀, y₀))

Si F diferenciable: Vector Normal: (-F´_u, -F´_w, 1) o (F´_u, F´_w,-1)

Plano tangente a una superficie: Definición: Dada S Ì R³ una superficie regular de ecuación vectorial x = G (u, w), (u, w)Ì A R ², se define el plano tangente a S en le punto A = G (u0, w0) como:

G´_u (u0, w0) x G´_w (u0, w0).(x - G (u0, w0)) = 0

Teorema: Dada F A Ì R ² ® R, A abierto, F diferenciable en x₀Ì A, entonces la ecuación del plano tangente al grafico de F en el punto (x₀, y₀, F (x₀, y₀)) es:

Z = F (x₀, y₀) + F´_x (x₀, y₀) (x-x₀) + F´_y (x₀, y₀) (y-y₀)

Observación: Con el mismo vector G´_u X G´_w se puede definir la recta normal a S:

x = λ (G´_u (u0, w0) x G´ (u0, w0)), λ Ì R

O bien la recta normal al grafico de F.

x = λ (-F´_x (x₀, w0), -F´y (x₀, y₀), 1) + (x₀, y₀, F (x₀, y₀)), λ Ì R

Composición de funciones:

Teorema: Dada F: A Ì Rⁿ ® R^m, diferenciable en A, G: bÌ R^m ® R^p, diferenciable en b, con F (A) Ì b, entonces:

D (g0f) (x₀) = Dg (f (x₀)). Df (x₀), x₀ Ì A. Se usan matrices Jacobiano.

Corolario: Dada F: A Ì Rⁿ ® R, diferenciables en A, entonces Ñ f (x₀) es perpendicular al conjunto de nivel f (x) = f (x₀), en le punto x₀.

R ²: ÑF (G (t)) ˆ G´ (t)

R³: ÑF (G (u, w)) ˆ al plano tangente a la superficie de nivel en el punto G (u, w)

Regla practica para derivar:

F = F (u, w)			u		x ® h´x = F´u u´x + F´w w´x	Con todos los caminos posibles que conducen a la variable de derivación
u = u (x, y)	resulta F	á
w = w (x, y)	h (x, y)		w		y ® h´y = F´u u´y + F´w w´y

x x = (x, y).(x, y) = x ² + y ² = |x| ²

Para diferenciablidad:

[F(x) - F(0) - ÑF(0).(x - 0)]/|x - 0|

"Como el grafico de F tiene recta normal en (1, 0, 1) entonces F es diferenciable en (1, 0)

Funciones definidas en forma explícita:

Teorema: F (x₀, y₀) = 0 y F´y (x₀, y₀) ≠ 0 Þ F (x, y) = 0 define localmente en forma implícita una única función Y = Y (x) tal que:

a) y (x₀) = y₀

b) y (x₀) = F_x(x₀, y₀)/F_y(x₀, y₀)

Z = f(x,y)

x + y.z - e^z = 0 ® F(x,y,z)

F´_z = y - e^z

Z´_x = -F´_x/F´_z = -1/(y - e^z)

Z"_xx = -e^z.z´_x /(y - e^z) ² = [-e^z/(y - e^z)³].z´_x = F´_y /F´_z

Extremos:

Absoluto: F (a) ≥ F (x) " x Local: F (a) ≥ F (x)" x Ì E (a)

Obs: punto frontera solo puede ser extremos absoluto.

Teorema: Si existe la derivada con respecto a un vector en un extremo entonces es cero.

Obs:

a)si para algún versor la derivada da ≠ 0 Þ no es extremo local

b)Si no $ F´ (a, ř) Þ nada puede asegurarse.

Teorema: F diferenciable /F (a) es extremo local, entonces debe ser ÑF (a) = 0 (punto crítico o estacionario)

Teorema: F diferenciable /ÑF (a) = 0 Þ F (a) es punto silla F (x1)≤ F (a)≥F (x2)

Matriz Hesiano: F Ì C ² /ÑF (a) = 0

F" xx (a)	F" xy (a)		det H (a) > 0 y F" xy (a) < 0 Υ F" yy (a) > 0 ÞF (a) es mínimo local
H (a) =	F" xy (a)	F" yy (a)	det H (a) > 0 y F" xx (a) < 0 Υ F" yy (a) < 0 ÞF (a) es máximo local
			det H (a) < 0 Þ F (a) punto silla
			det H (a) = 0 nada se sabe.

Casos de funciones escalares diferenciables

Derivadas máximas: řmáxima = ÑF (x₀); řmin = - ÑF (x₀)

En R ²: ř0 = (F´y (x₀), - F´x (x₀)) ř0 = (-F´y (x₀), F´x (x₀))

F´ (x₀, řmáxima) = |ÑF (x₀)| F´ (x₀, řmin) = -|ÑF (x₀)|

Desarrollo de Taylor: R ² ® R : a = (a1, a2)

F (x, y) =	d ²
= F (a1, a2) + F´x (a) (x-a1) + F´y (a) (y-a2) +	1/2[F" xx (a) (x-a1) ² + F" yy (a) (y-a2) ² + 2F" xy (a) (x-a1) (y-a2)]
+ 1/6[F"´ xxy (a) (x-a1)³ + F"´ (a) (y-a2)³ + 3F"´ xxy (a) (x-a1) ² (y-a2) + 3F"´ yyx (a) (x-a1) (y-a2) ²]
d³

Extremos condicionados:

Teorema (Lagrange - Para puntos críticos)

Dada F: A Ì Rⁿ ® R, A abierto, f Ì C ² y dadas Fi: AÌ Rⁿ — R, Fi Ì C ², 1≤ i≤ n con m < n.

Entonces los extremos locales de F sujetos a las condiciones Fi (x) = 0, 1≤ i = m, se pueden obtener estudiando los extremos locales de la siguiente función.