Tiro vertical o lanzamiento vertical
Movimiento uniformemente variado, donde la aceleración es la de la gravedad y la dirección del movimiento puede ser ascendente o descendente, sin influencia de la fricción con el aire.
a = g
v₀ ≠ 0
Este movimiento siempre tiene velocidad inicial distinta de cero, sea lanzado hacia arriba o hacia abajo.
Las ecuaciones para éste movimiento son:
1) yf = y₀ + v₀·t + ½·g·t² (Ecuación horaria de posición)
2) vf = v₀ + g·t (Ecuación horaria de velocidad)
3) vf² = v₀² + 2·g·Δy
Altura Máxima: El único instante donde la velocidad es nula es cuando alcanza la altura máxima, si el objeto o móvil fue lanzado hacia arriba. Es el punto donde el objeto se detiene y comienza el descenso.
Ecuaciones para el caso de calcular la altura máxima:
1) yₘₐₓ = y₀ + v₀·t + ½·g·t² (Ecuación horaria de posición)
2) 0 = v₀ + g·t (Ecuación horaria de velocidad)
3) 0 = v₀² + 2·g·Δy
Velocidad Inicial: Una particularidad del tiro vertical es que un objeto lanzado hacia arriba con una determinada velocidad inicial, al regreso y pasando por el mismo punto de partida, posee el mismo valor de velocidad pero con sentido contrario al del lanzamiento.
El valor de la aceleración de la gravedad depende del paralelo (latitud) en que se determine dicho valor. En el ecuador (latitud = 0) la aceleración es igual a "9,78049 m/s²", la aceleración promedio es de 9,81 m/s², resulta práctico usar un valor de 10 m/s² para agilizar la resolución de ejercicios.
Ejes convenientes para graficar el movimiento:
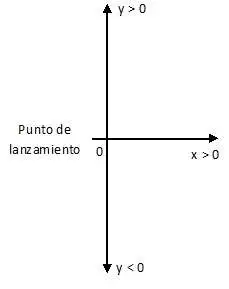
Orientación de los vectores y selección de los signos de las variables según la dirección del movimiento:
| Lanzamiento hacia … | Velocidad inicial | Aceleración (g) | ||
|---|---|---|---|---|
| Vector | Signo | Vector | Signo | |
| Arriba | ↑ | + | ↓ | - |
| Abajo | ↓ | - | ↓ | - |
Estos signos se deben aplicar cuando se reemplazan las variables por sus valores.
• Nota: si la velocidad inicial es nula (v₀ = 0) se trata de "Caída libre".
Autor: Ricardo Santiago Netto. Argentina
¿Cuál es la aceleración de la gravedad? ¿Cuál es el sentido de la aceleración de la gravedad?