Problema nº 10 de movimiento relativo - TP08

Enunciado del ejercicio nº 10

Una avioneta cuya velocidad respecto del aire es 205 km/h, pasa sobre la ciudad A, dirigiéndose hacia la ciudad B situada 400 km al norte de A. La oficina meteorológica en tierra le informa que sopla viento en dirección este-oeste, a 45 km/h.

a) Determinar la dirección en que se desplaza la avioneta en esas condiciones.

b) Hallar el ángulo que debe desviar su rumbo, para desplazarse efectivamente hacia B, suponiendo que se mantienen constantes las velocidades.

c) Hallar cuánto tardará en llegar.

Desarrollo

Datos:

vᵣ = 205 km/h

x = 400 km

v_viento = 45 km/h

Fórmulas:

Teorema de Pitágoras

h² = a² + b²

Esquema:

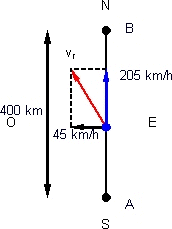
Esquema del movimiento relativo

Solución

a)

Aplicando trigonometría, la dirección con respecto al norte es:

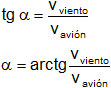
Reemplazamos por los valores y calculamos:

Resultado, la dirección en que se desplaza la avioneta es:

α = 12° 22' 51"

b)

El esquema es:

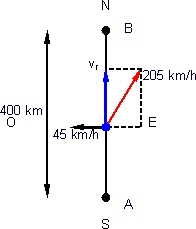
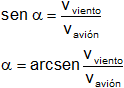
Reemplazamos por los valores y calculamos:

Resultado, el ángulo para corregir su rumbo es:

α = 12° 40' 49" en dirección NE

c)

Debemos calcular la velocidad en dirección S-N.

Aplicando el Teorema de Pitágoras:

v_avión² = v_viento² + v_SN²

Reemplazando:

Calculando:

v_SN = 200 km/h

Luego:

Reemplazamos por los valores y calculamos:

Resultado, el tiempo empleado para llegar al punto B es:

t = 2 h

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP08
• | Siguiente ›

Ejemplo, cómo resolver un problema de movimiento relativo. Nivel medio, secundaria, bachillerato, ESO.