Problema nº 3 de tiro o lanzamiento vertical, altura máxima y velocidad - TP12

Enunciado del ejercicio nº 3

Se lanza un cuerpo verticalmente hacia arriba, alcanzando una velocidad de 8 m/s al llegar a un tercio de su altura máxima.

a) ¿Qué altura máxima alcanzará?

b) ¿Cuál es su velocidad inicial?

c) ¿Cuál es la velocidad media durante el primer segundo del movimiento?

Usar g = 10 m/s²

Desarrollo

Datos:

v₀ = 8 m/s

h = ⅓·hₘₐₓ m

t = 1 s

Fórmulas:

v_f = v₀ + g·t (1)

y = v₀·t + ½·g·t² (2)

v_f² - v₀² = 2·g·h (3)

Esquema:

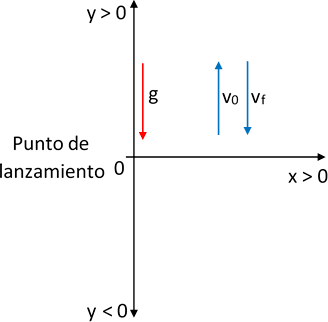
Sentido de los vectores en el tiro vertical hacia arriba

Solución

a)

Para la altura máxima v_f = 0, de la ecuación (3):

-v₀² = 2·g·h

Despejamos "h":

Reemplazamos por los datos y calculamos:

hₘₐₓ = 3,2 m (corresponde a ⅔ de la altura total).

Luego la altura total es:

h_T = 3,2 m + ½·3,2 m

Resultado, la altura máxima alcanzada es:

h = 4,8 m

b)

Mediante la ecuación (3):

v₀² = -2·g·h

v₀² = -2·(-10 m/s²)·(4,8 m)

Resultado, la velocidad inicial es:

v₀ = 9,8 m/s

c)

Primero calculamos el tiempo total con la ecuación (1) y para v_f = 0:

Reemplazamos por los valores y calculamos:

t = 0,98 s

Luego de alcanzar la altura máxima comienza el descenso, debemos averiguar la distancia que recorre en las 0,02 s restantes.

Empleamos la ecuación (2) con v₀ = 0 m/s, la aceleración será positiva:

y = ½·g·t²

y = ½·(10 m/s²)·(0,02 s)²

y = (5 m/s²)·0,0004 s²

y = 0,002 m

Sumando el desplazamiento hasta alcanzar la altura máxima y el desplazamiento de descenso de 0,02 s tenemos el desplazamiento total:

d = h + y

d = 4,8 m + 0,002 m

d = 4,802 m

Como:

Reemplazamos por los valores y calculamos:

Resultado, la velocidad media durante el primer segundo del movimiento es:

Δv = 4,802 m/s

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP12
• | Siguiente ›

Ejemplo, cómo calcular la altura máxima y la velocidad en el movimiento uniforme variado. Nivel medio, secundaria, bachillerato, ESO.