Problema nº 6 de tiro o lanzamiento vertical, altura máxima y velocidad - TP12
Enunciado del ejercicio nº 6
Un cuerpo es arrojado verticalmente hacia arriba y pasa por un punto a 36 m, por debajo del de partida, 6 s después de haber sido arrojado.
a) ¿Cuál fue la velocidad inicial del cuerpo?
b) ¿Qué altura alcanzó por encima del punto de lanzamiento?
c) ¿Cuál será la velocidad al pasar por un punto situado a 25 m por debajo del de lanzamiento?
Usar g = 10 m/s²
Desarrollo
Datos:
h = 36 m
t = 6 s
Fórmulas:
vf = v₀ + g·t (1)
y = v₀·t + ½·g·t² (2)
vf² - v₀² = 2·g·h (3)
Esquema:
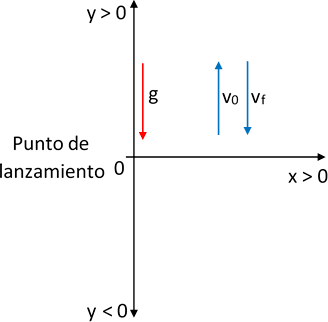
Sentido de los vectores en el tiro vertical hacia arriba
Solución
a)
Teniendo en cuenta que la velocidad al pasar por el punto de partida es igual que la velocidad inicial con sentido contrario.
Adaptando la ecuación (1) para lo ocurrido entre el lanzamiento y el retorno al punto de partida.
El tiempo de 6 s se compone del tiempo que demoro en alcanzar la altura máxima, más el tiempo que demoro en regresar al punto de partida, más el tiempo que empleo en caer 36 m bajo el punto de partida, planteando las ecuaciones (1) y (2) para cada etapa:
Subida:
(1) 0 = v₀₁ + g·t₁
(2) y₁ = v₀₁·t₁ + ½·g·t₁²
Regreso:
(1) vf2 = g·t₂
(2) y₂ = ½·g·t₂²
Bajando 36 m:
(1) vf3 = v₀₃ + g·t₃
(2) y₃ = v₀₃·t₃ + ½·g·t₃²
Luego:
t₁ + t₂ + t₃ = 6 s
También:
t₁ = t₂
Por lo que:
2·t₁ + t₃ = 6 s
También sabemos que:
v₀₃ = vf2 = -v₀₁
Reemplazando en la ecuación (2) de "bajando 36 m":
y₃ = -v₀₁·t₃ + ½·g·t₃²
Continuando:
t₁ = ½·(6 s - t₃)
y₃ = ½·g·(6 s - t₃)·t₃ + ½·g·t₃²
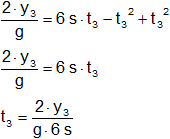
Reemplazamos por los valores y calculamos:
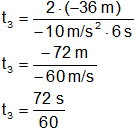
t₃ = 1,2 s
t₁ = ½·(6 s - 1,2 s)
t₁ = 2,4 s
t₂ = 2,4 s
Con la ecuación (1) de "Subida":
v₀₁ = -g·t₁
v₀₁ = -(-10 m/s²)·(2,4 s)
Resultado, la velocidad inicial del cuerpo es:
v₀₁ = 24 m/s
b)
Con la ecuación (2) de "Subida":
y₁ = (24 m/s)·(2,4 s) + ½·(-10 m/s²)·(2,4 s)²
Resultado, la altura máxima alcanzada es:
y₁ = 28,8 m
c)
Con la ecuación (3):
vf² = (24 m/s)² + 2·(10 m/s²)·(25 m)
Resultado, la velocidad al pasar por un punto situado a 25 m por debajo del de lanzamiento es:
vf = 32,8 m/s (hacia abajo)
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP12
- | Siguiente ›
Ejemplo, cómo calcular la altura máxima y la velocidad en el movimiento uniforme variado. Nivel medio, secundaria, bachillerato, ESO.