Problema nº 6 de caída libre, velocidad y altura - TP14
Enunciado del ejercicio nº 6
Se deja caer una piedra en un pozo y al cabo de 10 s se oye el choque contra el fondo, si la velocidad del sonido es de 330 m/s, ¿cuál es la profundidad del pozo?
Usar g = 10 m/s²
Desarrollo
Datos:
vsonido = 330 m/s
t = 10 s
Fórmulas:
vf = g·t (1)
Δh = ½·g·t² (2)
Solución
El tiempo es el tiempo total, es decir el que tarda la piedra en caer más el que tarda el sonido en llegar hasta el punto de partida de la piedra:
t = tₚ + tₛ = 10 s ⇒ tₛ = 10 s - tₚ (3)
La distancia que recorre el sonido es igual a la distancia que recorre la piedra:
ΔhT = Δhₛ = Δhₚ (4)
Para el sonido:
vₛ = Δhₛ/tₛ
Δhₛ = vₛ·tₛ (5)
Para la piedra.
Δhₚ = ½·g·tₚ² (6)
Igualando (5) y (6):
vₛ·tₛ = ½·g·tₚ² (7)
Reemplazando (3) en (7):
Vₛ·(10 s - tₚ) = ½·g·tₚ²
10 s·Vₛ - Vₛ·tₚ = ½·g·tₚ²
½·g·tₚ² + Vₛ·tₚ - 10 s·Vₛ = 0
Reemplazando por los datos:
½·(9,81 m/s²)·tₚ² + (330 m/s)·tₚ - 10 s·(330 m/s) = 0
(4,905 m/s²)·tₚ² + (330 m/s)·tₚ - 3.300 m = 0
Resolvemos la ecuación cuadrática (Báscara o Bhaskara):
| tp-1,2 = | -330 m/s ± √(330 m/s)² - 4·4,905 m/s²·(-3.300 m) |
| 2·4,905 m/s² |
| tp-1,2 = | -330 m/s ± √108.900 m²/s² + 647.460 m²/s² |
| 9,81 m/s² |
| tp-1,2 = | -330 m/s ± √173.646 m²/s² |
| 9,81 m/s² |
| tp-1,2 = | -330 m/s ± 416,71 m/s |
| 9,81 m/s² |
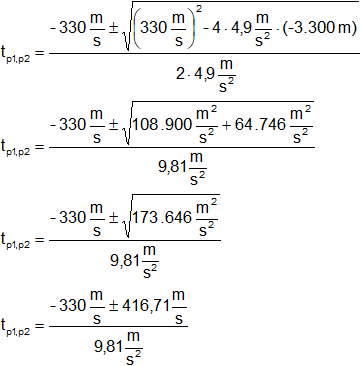
Presentamos las dos ecuaciones, una por cada signo:
| tₚ₋₁ = | -330 m/s + 416,71 m/s |
| 9,81 m/s² |
| tₚ₋₂ = | -330 m/s - 416,71 m/s |
| 9,81 m/s² |
Resolvemos:
| tₚ₋₁ = | 86,71 m/s |
| 9,81 m/s² |
| tₚ₋₂ = | -746,71 m/s |
| 9,81 m/s² |
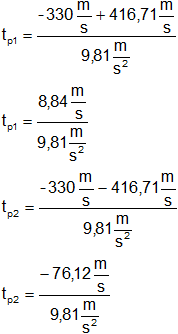
tₚ₋₁ = 8,84 s
tₚ₋₂ = -76,12 s
tₚ₋₂ lo descartamos porque el tiempo negativo no existe. En la ecuación (6) reemplazamos con tₚ₋₁ y resolvemos:
Δhₚ = ½·(9,81 m/s²)·(8,84 s)²
Δhₚ = (4,905 m/s²)·(78,15 s²)
Resultado, la profundidad del pozo es:
Δhₚ = 383,3 m
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP14
- | Siguiente ›
Ejemplo, cómo calcular la velocidad y la altura en el movimiento uniforme variado. Nivel medio, secundaria, bachillerato, ESO.