Problema nº 5 de tiempo y distancia en el movimiento uniformemente variado (MUV) - TP16

Enunciado del ejercicio nº 5

Un móvil que pasa en línea recta hacia la derecha de un punto "a", animado de un MUV, con una velocidad de 8 m/s y una aceleración de 2 m/s², pero en sentido contrario. Luego regresa inmediatamente. Determinar:

a) ¿Después de cuánto tiempo se detiene?

b) ¿A qué distancia de "a" lo logra?

c) ¿Cuánto tarda en volver a pasar por "a"?

d) ¿En qué instante pasa por un punto situado a 15 m a la derecha de "a"?

e) ¿En qué instante pasa por un punto situado a 33 m a la izquierda de "a"?

Desarrollo

Datos:

v₀ = 8 m/s

v_f = 0 m/s

a = -2 m/s²

x₁ = 15 m

x₂ = -33 m

Fórmulas:

v_f = v₀ + a·t (1)

x = v₀·t + ½·a·t² (2)

v_f² - v₀² = 2·a·Δx (3)

Esquema:

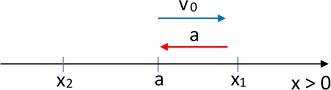
Sentido de los vectores en el movimiento

Solución

a)

De la ecuación (1) despejamos el tiempo:

v_f = v₀ + a·t

0 = v₀ + a·t

-v₀ = a·t

Reemplazamos por los datos y calculamos:

Resultado, el móvil se detiene luego de:

t = 4 s

b)

De la ecuación (3) obtenemos la distancia recorrida:

v_f² - v₀² = 2·a·Δx

0 - v₀² = 2·a·Δx

-v₀² = 2·a·Δx

Reemplazamos por los datos y calculamos:

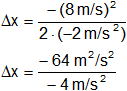
Resultado, la distancia a a que el móvil se detendrá es:

Δx = 16 m

c)

De la ecuación (1) despejamos el tiempo:

v_f = v₀ + a·t

Esta vez la velocidad inicial es nula y la velocidad final tendrá sentido contrario.

v_f = 0 + a·t

v_f = a·t

Reemplazamos por los datos y calculamos:

Resultado, el tiempo que demorará el móvil en volver a pasar por "a" es:

t = 4 s

d)

De la ecuación (2) despejamos el tiempo para x₁:

x₁ = v₀·t + ½·a·t²

Igualamos a cero:

½·a·t² + v₀·t - x₁ = 0

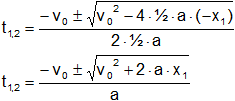
Reemplazamos por los datos y calculamos:

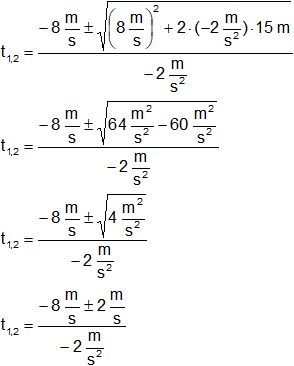
t_1,2 = 4 s ∓ 1 s

t₁ = 4 s - 1 s

t₂ = 4 s + 1 s

Resultado, el instante en que el móvil pasa por un punto situado a 15 m a la derecha de "a" es:

t₁ = 3 s

t₂ = 5 s (a la izquierda del punto "a")

e)

De la ecuación (2) despejamos el tiempo para x₂:

x₂ = v₀·t + ½·a·t²

Igualamos a cero:

½·a·t² + v₀·t - x₂ = 0

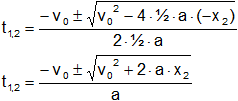
Reemplazamos por los datos y calculamos:

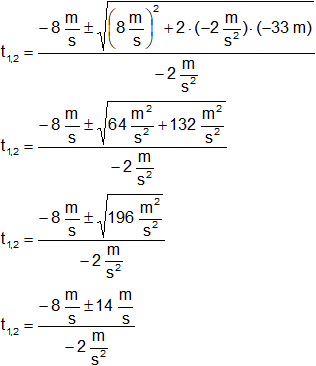
t_1,2 = 4 s ∓ 7 s

t₁ = 4 s - 7 s

t₂ = 4 s + 7 s

Resultado, el instante en que el móvil pasa por un punto situado a 33 m a la izquierda de "a" es:

t₁ = -3 s (No es solución)

t₂ = 11 s

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP16
• | Siguiente ›

Ejemplo, cómo calcular el tiempo y la distancia. Nivel medio, secundaria, bachillerato, ESO.