Problema nº 9 de desplazamiento y velocidad media en el movimiento uniformemente variado (MUVR) - TP16
Enunciado del ejercicio nº 9
Una partícula se mueve con MRUV retardado y aceleración (15 m/s² N15°E). Si a t = 0, la partícula se encuentra en la posición (-2, 3) m y su rapidez es de 8 m/s. Para un intervalo entre 0 y 8 s; determinar:
a) El desplazamiento realizado.
b) La velocidad media.
Desarrollo
Datos:
a = 15 m/s²
α = 15°
El punto de origen es (-2, 3), o sea:
x₀ = -2 m
y₀ = 3 m
v₀ = 8 m/s
Fórmulas:
Vf = V₀ + a·t (1)
Δd = V₀·t + ½·a·t² (2)
Esquema:
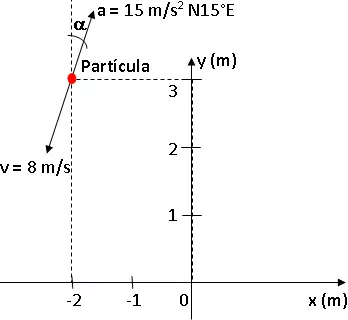
Solución
a)
Si bien el esquema parece complicado, la solución es más sencilla.
De la ecuación (2):
Δd = V₀·t + ½·a·t²
Δd = (8 m/s)·8 s + ½·(-15 m/s²)·(8 s)²
Δd = 64 m - 480 m
Δd = - 416 m
¡Una distancia negativa! El resultado parece correcto aunque no indica qué tipo de recorrido es. Ver más abajo.
b)
Para calcular la velocidad media, primero, hay que calcular la velocidad final; de la ecuación (1):
Vf = V₀ + a·t
Vf = 8 m/s + (-15 m/s²)·(8 s)
Vf = 8 m/s -120 m/s
Vf = -112 m/s
Ahora tenemos una velocidad negativa, correcto. La partícula se dirigió, primero, hacia NE, hasta que se detuvo y, con la misma aceleración negativa, luego se dirigió por el mismo camino, pero en sentido contrario (SO).
La velocidad media es el promedio entre la velocidad inicial y la final:
Vₘ = ½·(Vf - V₀)
Vₘ = ½·(-112 m/s - 8 m/s)
Vₘ = 60 m/s
El enunciado pide velocidad media y desplazamiento, por lo tanto, aquí concluye el ejercicio.
Un paso más, ¿qué ocurrió durante el movimiento?
Hay un momento en que la partícula se detiene, es decir vf = 0 m/s, con la ecuación (1) hallamos ese instante
Vf = V₀ + a·t
0 = V₀ + a·t
a·t = -V₀
t = -V₀/a
t = -(8 m/s)/(-15 m/s²)
t = 0,533 s
La distancia recorrida será:
Δd = V₀·t + ½·a·t²
Δd = (8 m/s)·0,533 s + ½·(-15 m/s²)·(0,533 s)²
Δd = 4,264 m - 2,133 m
Δd = 2,133 m
En el tiempo t = 0,533 s la partícula se detuvo luego de recorrer 2,13 m, a partir de ahí comenzó a moverse en sentido contrario (SO) con aceleración -15 m/s².
¿En qué lugar se encuentra a los 8 s?
Repetimos los cálculos pero tomando como datos iniciales los nuevos resultados.
V₀ = 0 m/s
t = 0,533 s
d₀ = 2,133 m
Solución:
El tiempo transcurrido será:
Δt = 8 s - 0,533 s = 7,467 s
La posición:
Δd = V₀·t + ½·a·t²
Δd = 0 + ½·(-15 m/s²)·(7,467 s)²
Δd = -418,17 m
Es decir, recorrió ésta distancia desde que se detuvo, por lo tanto, hay que sumarle la distancia recorrida inicialmente, en valor absoluto.
Δd = 2,33 m + 418,17 m
Δd = 420 m (Este es el recorrido total, no el desplazamiento final)
Ahora, mediante la trigonometría, hallamos la posición, pero con el desplazamiento desde el punto (Δd = 416 m).
sen α = Δx/Δd ⇒ Δx = Δd·sen α ⇒ Δx = -416 m·sen 15° ⇒ Δx = -107,7 m
cos α = Δy/Δd ⇒ Δy = Δd·cos α ⇒ Δy = -416 m·cos 15° ⇒ Δy = -401,8 m
Resultado, el punto es (-107,7; -401,8) m
Enviado por: Alejandra
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP16
- | Siguiente ›
Ejemplo, cómo calcular el desplazamiento y la velocidad media. Nivel medio, secundaria, bachillerato, ESO.