Problema nº 8 de tiro o lanzamiento vertical, tiempo - TP17
Enunciado del ejercicio nº 8
Se lanza un balón verticalmente hacia arriba con una velocidad v₀, t segundos después, y desde la misma altura se lanza un segundo balón también verticalmente hacia arriba a igual velocidad v₀.
Calcular cuánto tiempo medido a partir del lanzamiento del segundo balón, se demora la colisión entre ellos.
Desarrollo
Fórmulas:
y = v₀·t + ½·g·t²
Solución
Ambos balones partieron con la misma velocidad inicial, por lo tanto, lo balones colisionaran luego de que el primero alcance su altura máxima y se encuentre de regreso, asumiendo que ambos balones sigan la misma trayectoria.
Para el primer balón:
y₁ = v₁₀·t₁ + ½·g·t₁² [1]
Para el segundo balón:
y₂ = v₂₀·t₂ + ½·g·t₂² [2]
Pero:
v₁₀ = v₂₀
Entonces:
y₁ = v₀·t₁ + ½·g·t₁² [1]
y₂ = v₀·t₂ + ½·g·t₂² [2]
Debemos tener en cuenta que:
t = t₁ - t₂ (t es el tiempo buscado)
Despejamos t₁ y la reemplazamos en la ecuación [1]:
t₁ = t + t₂
y₁ = v₀·(t + t₂) + ½·g·(t + t₂)² [1]
y₂ = v₀·t₂ + ½·g·t₂² [2]
Cuando la posición y₂ = y₁ (pero en sentido contrario), ocurrirá el encuentro:
v₀·t₂ + ½·g·t₂² = v₀·(t + t₂) + ½·g·(t + t₂)²
Trabajamos algebraicamente:
v₀·t₂ + ½·g·t₂² = v₀·(t + t₂) + ½·g·(t² + 2·t·t₂ + t₂²)
v₀·t₂ + ½·g·t₂² = v₀·t + v₀·t₂ + ½·g·t² + ½·g·2·t·t₂ + ½·g·t₂²
0 = v₀·t + ½·g·t² + g·t·t₂
0 = v₀·t + g·t·t₂ + ½·g·t²
Y obtenemos una ecuación de segundo grado:
0 = (v₀ + g·t₂)·t + ½·g·t²
Aplicamos la ecuación cuadrática (Báscara o Bhaskara) que dará dos resultados:
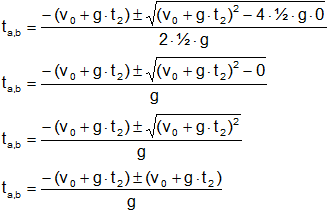
Separamos las ecuaciones una por cada signo y resolvemos:
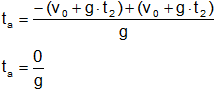
tₐ = 0

Por lo tanto tₐ se descarta porque sería el mismo instante.
tb es el valor buscado, lo expresamos:
![]()
Enviado por: @sebastiayala.
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP17
- | Siguiente ›
Ejemplo, cómo calcular el tiempo en el movimiento uniforme variado. Nivel medio, secundaria, bachillerato, ESO.