Problema nº 6 de movimiento circular en el plano, aceleración angular - TP19
Enunciado del ejercicio nº 6
Calcular la aceleración angular de una rueda de 0,25 m de radio, al lograr a los 20 s, una velocidad de 40 km/h.
Desarrollo
Datos:
t = 20 s
r = 0,25 m
v₁ = 0 m/s
v₂ = 40 km/h
Fórmulas:
| v = | 2·π·r | (1) |
| T |
| ω = | 2·π | (2) |
| T |
ω₂ = ω₁ ± α·t (3)
Solución
Aplicamos la ecuación (1) para hallar el período T:
| v = | 2·π·r |
| T |
| T = | 2·π·r |
| v |
Reemplazamos T en la ecuación de la velocidad angular (2):
| ω = | 2·π |
| T |
| ω = | 2·π |
| 2·π·r | |
| v |
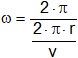
| ω = | v | (4) |
| r |
Aplicamos la ecuación horaria de velocidad angular (3):
ω₂ = ω₁ ± α·t
ω₁ = 0
ω₂ = ±α·t
La velocidad angular aumenta, por tanto:
ω₂ = α·t (5)
Luego, de (4):
| ω₂ = | v₂ |
| r |
Igualamos con (5):
| α·t = | v₂ |
| r |
Despejamos la aceleración angular α:
| α = | v₂ |
| t·r |
Adecuamos las unidades:
| v₂ = 40 km/h· | 1.000 m | · | 1 h |
| 1 km | 3.600 s |
v₂ = 11,11 m/s
Reemplazamos y calculamos:
| α = | 11,11 m/s |
| 20 s·0,25 m |
| α = | 11,11 |
| 5 s² |
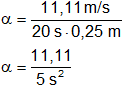
α = 2,222222222 /s
Resultado, la aceleración angular es:
α = 2,22/s
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP19
- | Siguiente ›
Ejemplo, cómo calcular la aceleración angular en el movimiento circular uniforme. Nivel medio, secundaria, bachillerato, ESO.