Problema nº 2 de encuentro, lugar y tiempo de encuentro - TP20

Enunciado del ejercicio nº 2

Resolver el problema anterior, suponiendo que el primer móvil partió 0,1 s antes que el otro.

Desarrollo

Datos:

d_AB = 100 m

t_AB = 2 s

t_BA = 1,5 s

Fórmulas:

(1)

(2)

Solución

El tiempo empleado por el móvil A para recorrer los 100 m es el mismo, solamente comenzó 0,1 s antes, por lo tanto, cuando el móvil B comienza su recorrido, el móvil A ya recorrió cierto espacio. De la ecuación (1):

v_AB = (100 m)/(2 s)

v_AB = 50 m/s

La distancia inicial es:

Δd = v_AB·(0,1 s)

Δd = (50 m/s)·(0,1 s)

Δd = 5 m

a)

Para el punto de encuentro:

d_AB = d_AO + 5 m + d_BO (3)

Siendo el punto O el punto de encuentro.

Como ambos comienzan su movimiento en el mismo instante el tiempo de encuentro es el mismo para ambos móviles.

t_AO - 0,1 s = t_BO = t_E

Luego contiuamos como en el ejercicio (1):

Para el encuentro las (1) y (2) ecuaciones quedan:

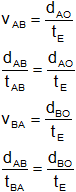
Despejamos (t_E) y luego igualamos:

(4)

(5)

t_AB·d_AO = t_BA·d_BO

De la ecuación (3):

d_AO = d_AB - d_BO - 5 m

t_AB·(d_AB - d_BO - 5 m) = t_BA·d_BO

t_AB·d_AB - t_AB·d_BO - t_AB·(5 m) = t_BA·d_BO

t_AB·d_AB - t_AB·(5 m) = t_AB·d_BO + t_BA·d_BO

t_AB·(d_AB - 5 m) = (t_AB + t_BA)·d_BO

Reemplazamos por los valores y calculamos:

Resultado, el punto de encuentro es:

d_BO = 54,29 m (desde el punto B)

ó

d_AO = 45,71 m (desde el punto A)

b)

Empleando la ecuación (4) ó (5):

Resultado, el momento del encuentro es:

t_E = 0,81 s

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP20
• | Siguiente ›

Ejemplo, cómo calcular el lugar y tiempo de encuentro en el movimiento uniforme variado. Nivel medio, secundaria, bachillerato, ESO.