Problema nº 3 de encuentro, distancia y tiempo luego del encuentro - TP20

Enunciado del ejercicio nº 3

Se tira una bolita A con una velocidad de 10 m/s y en el mismo momento pero, 5 m más adelante, se tira una bolita B con una velocidad de 8 m/s.

a) ¿Cuánto tiempo después la bolita A pasa a la B?

b) ¿A qué distancia de la posición inicial de la bolita B?

v_A = 10 m/s

v_B = 8 m/s

d = 5 m

(1)

(2)

Para la distancia:

d_A - 5 m = d_B (3)

Las ecuaciones (1) y (2) para el encuentro:

(4)

(5)

Despejando d_A e igualando:

v_A·t_E = d_A

v_B·t_E + 5 m = d_A

v_A·t_E = v_B·t_E + 5 m

v_A·t_E - v_B·t_E = 5 m

(v_A - v_B)·t_E = 5 m

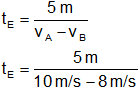
Cálculo del tiempo

Resultado, el tiempo encuentro entre la bolita A y la B es:

t_E = 2,5 s

De la ecuación (4):

d_A = (10 m/s)·(2,5 s)

d_A = 25 m

De la ecuación (3):

d_B = 25 m - 5 m

Resultado, la distancia recorrida por la bolita B hasta el encuentro es:

d_B = 20 m

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular la distancia y tiempo luego del encuentro en el movimiento uniforme variado. Nivel medio, secundaria, bachillerato, ESO.