Problema nº 2 de aceleración, tiempo y posición en el movimiento uniformemente variado (MUV) - TP21

Enunciado del ejercicio nº 2

Un automóvil parte del reposo y adquiere una velocidad de 40 m/s en 15 s, calcular:

a) La aceleración.

b) Si éste sigue aumentando la velocidad al mismo ritmo, ¿cuántos segundos más necesitara para alcanzar una velocidad de 60 m/s?

c) Las distancias recorridas en los puntos anteriores.

Desarrollo

Datos:

v₀ = 0 m/s

v_f1 = 40 m/s

v_f2 = 60 m/s

t = 15 s

Fórmulas:

v_f = v₀ + a·t (1)

x = v₀·t + ½·a·t² (2)

v_f² - v₀² = 2·a·Δx (3)

Esquema:

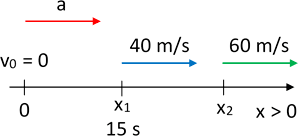
Diagrama de los vectores velocidad y aceleración en MRUV

Solución

a)

De la ecuación (1) despejamos la aceleración:

v_f1 = v₀ + a·t

v_f1 = 0 + a·t

Reemplazamos con los datos y calculamos:

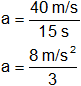
Resultado, la aceleración empleada es:

a = 2,67 m/s²

b)

De la ecuación (1) despejamos el tiempo para v_f2:

v_f2 = v₀ + a·t

En éste caso la velocidad inicial será v_f1:

v_f2 = v_f1 + a·t

v_f2 - v_f1 = a·t

Reemplazamos con los datos y calculamos. Usamos la aceleración hallada en el ítem anterior.

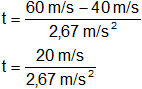
Resultado, el tiempo empleado para alcanzar una velocidad de 60 m/s es:

t = 10 s

c)

Empleamos la ecuación (2) y la aceleración hallada en el ítem (a):

x = v₀·t + ½·a·t²

Reemplazamos con los datos y calculamos:

x = 0 m/s·15 s + ½·(2,67 m/s²)·(15 s)²

x = ½·(2,67 m/s²)·225 s²

Resultado, la distancia recorrida hasta alcanzar la velocidad de 40 m/s es:

x = 300 m

Para segunda etapa utilizamos la ecuación (3) y la velocidad inicial será 40 m/s:

v_f2² - v_f1² = 2·a·Δx

Despejamos Δx:

Reemplazamos con los datos y calculamos:

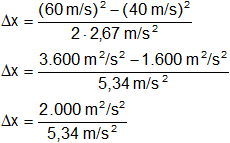
Resultado, la distancia recorrida desde que alcanzó los 40 m/s hasta que alcanzó los 60 m/s es:

x = 375 m

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP21
• | Siguiente ›

Ejemplo, cómo calcular la aceleración, el tiempo y la posición en el movimiento uniforme variado. Nivel medio, secundaria, bachillerato, ESO.