Problema nº 4 de velocidad final, tiempo y posición en el movimiento uniformemente variado (MUV) - TP21

Enunciado del ejercicio nº 4

Un cuerpo que parte del reposo se mueve en línea recta con aceleración constante y cubre una distancia de 64 m en 4 s. Determinar:

a) ¿Cuál fue su velocidad final?

b) ¿Qué tiempo tardó en recorrer la mitad de la distancia total?

c) ¿Cuál fue la distancia recorrida en la mitad del tiempo total?

d) ¿Cuál era su velocidad cuando había recorrido la mitad de la distancia total?

e) ¿Cuál era la velocidad al cabo de un tiempo igual a la mitad del total?

Desarrollo

Datos:

x = 64 m

t = 4 s

v₀ = 0 m/s

x_b = ½·x = 32 m

t_c = ½·t = 2 s

Fórmulas:

v_f = v₀ + a·t (1)

x = v₀·t + ½·a·t² (2)

v_f² - v₀² = 2·a·Δx (3)

Esquema:

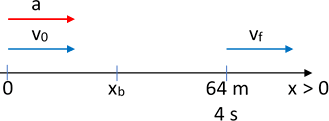
Diagrama de los vectores velocidad y aceleración en MRUV

Solución

a)

De la ecuación (2) despejamos la aceleración:

x = v₀·t + ½·a·t²

x = 0·t + ½·a·t²

x = ½·a·t²

Reemplazamos con los datos y calculamos:

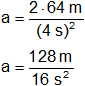
a = 8 m/s²

Con el dato de la aceleración aplicamos en la ecuación (1):

v_f = v₀ + a·t

v_f = 0 + a·t

v_f = a·t

v_f = 8 m/s²·4 s

Resultado, la velocidad final es:

v_f = 32 m/s

b)

Empleamos la ecuación (2) para hallar el tiempo en "x_b":

x_b = v₀·t + ½·a·t²

x_b = 0·t + ½·a·t²

x_b = ½·a·t²

Reemplazamos con los datos y calculamos:

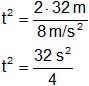
t² = 8 s²

La raíz cuadrada arroja dos resultados:

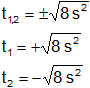
t₁ = 2,83 s

t₂ = -2,82 s (No es solución porque no existe el tiempo negativo)

Resultado, el tiempo requerido para recorrer la mitad de la distancia total es:

t = 2,83 s

c)

Empleamos la ecuación (2) para hallar al distancia en "t_c":

x_c = v₀·t_c + ½·a·t_c²

x_c = 0·t_c + ½·a·t_c²

x_c = ½·a·t_c²

Reemplazamos por los datos y calculamos:

x_c = ½·8 m/s²·(2 s)²

x_c = 4 m/s²·4 s²

Resultado, la distancia recorrida en la mitad del tiempo total es:

x_c = 16 m

d)

Empleamos la ecuación (3) para hallar la velocidad en "x_b":

v_fb² - v₀² = 2·a·x_b

v_fb² - 0² = 2·a·x_b

v_fb² = 2·a·x_b

v_fb = ±√2·a·x_b

La raíz cuadrada arroja dos resultados, se tomará el valor positivo ya que el cuerpo se mueve en el sentido positivo del eje "X":

v_fb = √2·a·x_b

Reemplazamos por los datos y calculamos:

v_fb = √2·8 m/s²·32 m

v_fb = √512 m²/s²

Resultado, la velocidad cuando había recorrido la mitad de la distancia total es:

v_fb = 22,63 m/s

e)

Empleamos la ecuación (1) para hallar al velocidad en "t_c":

v_fc = v₀ + a·t_c

v_fc = 0 + a·t_c

v_fc = a·t_c

Reemplazamos por los datos y calculamos:

v_fc = 8 m/s²·2 s

Resultado, la velocidad a la mitad del tiempo total es:

v_fc = 16 m/s

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP21
• | Siguiente ›

Ejemplo, cómo calcular la velocidad final, el tiempo y la posición en el movimiento uniforme variado. Nivel medio, secundaria, bachillerato, ESO.