Problema nº 5 de aceleración, tiempo y distancia en el movimiento uniformemente variado (MUV) - TP21

Enunciado del ejercicio nº 5

La velocidad de un automóvil que va hacia el norte se reduce de 30 m/s a 20 m/s en una distancia de 125 m. Determinar:

a) La magnitud y el sentido de la aceleración supuesta constante.

b) El tiempo transcurrido.

c) ¿Cuál fue la distancia recorrida con ésta aceleración desde el momento en que liberó los frenos?

Desarrollo

Datos:

v₀ = 30 m/s

v_f1 = 20 m/s

v_f2 = 0 m/s

Δx = 125 m

Fórmulas:

v_f = v₀ + a·t (1)

x = v₀·t + ½·a·t² (2)

v_f² - v₀² = 2·a·Δx (3)

Esquema:

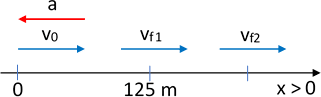
Diagrama de los vectores velocidad y aceleración en MRUV

Solución

a)

De la ecuación (3) despejamos la aceleración:

v_f1² - v₀² = 2·a·Δx

Reemplazamos con los datos y resolvemos:

Resultado, el sentido de la aceleración es hacia el sur y la magnitud es:

a = -2 m/s²

b)

Dado que tenemos el valor de la aceleración empleamos la ecuación (1) para hallar el tiempo:

v_f1 = v₀ + a·t

v_f1 - v₀ = a·t

Reemplazamos con los datos y calculamos:

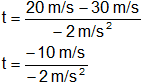
Resultado, el tiempo requerido para recorrer la distancia de frenado es:

t = 5 s

c)

Al liberar los frenos el automóvil continúa desacelerando de forma constante hasta detenerse.

Empleamos la ecuación (3) despejamos la distancia:

v_f2² - v_f1² = 2·a·Δx

-v_f1² = 2·a·Δx

Reemplazamos con los datos y resolvemos:

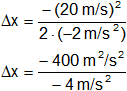
Resultado, la distancia recorrida desde que soltó los frenos hasta que se detuvo es:

Δx = 100 m

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP21
• | Siguiente ›

Ejemplo, cómo calcular la aceleración, el tiempo y la distancia en el movimiento uniforme variado. Nivel medio, secundaria, bachillerato, ESO.