Problema nº 1 de tiempo en un viaje espacial en el movimiento uniformemente variado (MUV)
Enunciado del ejercicio nº 1
Se quiere hacer un viaje a la estrella más cercana para investigar los planetas que se encuentran en la misma posición que la tierra a nuestro sol, por lo tanto, se realizara un viaje a la constelación de alfa centauri a una de sus estrellas llamada próxima centauri, que se encuentra a 4,2 años luz (aproximadamente). Queremos, para la comodidad del viajero, viajar con una aceleración constante y similar a la de la tierra (9,81 m/s²). El viaje no tiene que superar la mitad de la velocidad de la luz.
¿Cuánto tiempo le costará a la nave ir y venir, sin contar el tiempo de investigación, desde el punto de vista para nosotros?
Desarrollo
Datos:
Aceleración = 9,81 m/s²
Velocidad máxima = ½·c (c = velocidad de la luz)
Velocidad inicial = 0 = v₀
Tiempo inicial = 0 = t₀
Tiempo final = ?
Fórmulas:
| a = | dv |
| dt |
vf = v₀ + a·t
x = v₀·t + ½·a·t²
Solución
Dividiremos el viaje en 3 partes la parte donde aceleramos para alcanzar la mitad de c, donde desaceleramos a partir de la mitad de c, y la parte donde la velocidad es constante o sea a la mitad de c.
Primera parte:
Necesitamos alcanzar la mitad de c, por lo tanto, utilizaremos ecuaciones de movimiento rectilíneo uniformemente acelerado.
Tenemos: a = Constante
| a = | dv |
| dt |
dv = a·(dt)
Integrando y Resolviendo con valores iníciales
| ∫ | c/2 | dv = a·∫ | t | dt |
| v₀ | t₀ |
Por lo tanto:
½·c = a·t = velocidad máxima.
Ahora si calculamos cuanto tiempo nos tardara para llegar a c/2 con aceleración constante.
Por lo tanto:
t = ½·c/a = 15.290.519,88 s
Ahora calcularemos la distancia que se recorrió por haber acelerado constantemente.
| dv | = a = constante |
| dt |
Resolviendo
| ∫ | c/2 | dv = a·∫ | t₁ | dt |
| v₀ | t₀ |
v - v₀ = a·t
Donde v₀ es velocidad inicial, sustituimos v:
| dx | - v₀ = a·t |
| dt |
Entonces resolviendo tenemos que:
| ∫ | x | dx = ∫ | t | (v₀ + a·t)·dt |
| x₀ | t₀ |
x = x₀ + v₀·t + ½·a·t²
Sustituyendo valores iníciales tenemos que:
x = ½·a·t² = 1,146788991·10¹⁵ metros
Como tenemos el tiempo y la aceleración entonces podemos deducir la distancia que se recorrería en dicho intervalo.
Otra forma de hacerlos es:
a·dx = v·dv
a·(x - x₀) = ½·v² - ½·v₀²
Evaluando de 0 a ½·c y sustituyendo valores iníciales como v₀ = 0 y x₀ = 0 tenemos:
x = ½·v²/a = ⅛·c²/8
x = 1,146788991·10¹⁵ metros = 0,1212147872 años luz
A esta distancia no aceleraríamos más ya que estamos a la mitad de la velocidad de la luz.
Pero consideramos que próxima centauri se encontraba a 4,2 años luz por lo tanto:
Nos queda recorrer 3,957570426 años luz (restándole el doble de la distancia antes resuelta ya que antes de llegar desaceleraríamos a 9,81 m/s²)
Entonces:
v = d/t y t = d/v
| t = | 3,744178228·10¹⁶ |
| 3·10⁸·0,5 |
t = 249.611.881,9 s
Este es el tiempo que nos tomaría recorrer la distancia en la cual no aceleramos.
El tiempo total de ida y venida seria de la suma del tiempo en donde a = 0 y el tiempo para llegar a c/2 además de multiplicar este ultimo por 2 (por la desaceleración)
Entonces tenemos que el tiempo de ida es de: 280.192.921,7 s
Por lo tanto el tiempo de viaje seria el doble: 560.385.843,3 s o lo que es más bien: 17,76971852 años
Es demasiado tiempo pero sería posible. Como anexo agrego el tiempo que ocurriría dentro de la nave espacial ya que la relatividad de Einstein nos dice que cuanto más cerca nos acerquemos a la luz, el tiempo se hace más lento, el tiempo deja de transcurrir a la misma rapidez que en la tierra.
Definimos entonces: dt = tiempo del observador o sea de las personas que se quedarían en la tierra esperando el viaje de la nave espacial y dt₀ el tiempo dentro de la nave. Donde v será la velocidad de la nave en a = 0.
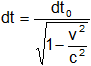dt = dt₀/√1 - v²/c² (ec.1)
Sustituyendo y despejando dt₀ y resolviendo tenemos:
dt₀ = 216.170.230,8 s
Ahora a = 9,81 m/s²
Por movimiento rectilíneo uniforme acelerado a = dv/dt
Entonces resolviendo v = v₀ + a·t y sustituyendo en v resolvemos ec.1:
dt₀ = 13.241.978,65 s
Multiplicando el primero por 2 y el segundo por 4 y sumándolos tenemos que el viaje dentro de la nave es de:
96.201.962,2 = 15,38902766 años.
Algo considerable para un viaje de tal magnitud, pero si viajáramos todavía más rápido hasta 0,9 de la velocidad de la luz solo nos tardaríamos 10,6 años en el viaje, desde el punto del observador en la tierra, pero dentro de ella seria unos 2,8 años, algo muy considerable para el viaje.
Autor: Ortiz Israel Raymundo. México.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
Ejemplo, cómo calcular tiempo en un viaje espacial. Nivel medio, secundaria, bachillerato, ESO.