Guía nº 29 de ejercicios de movimiento relativo

Resolver los siguientes ejercicios

Problema nº 1

Un tren pasa por una estación a 80 km/h, dentro del mismo, una persona se desplaza por el tren en el mismo sentido a 5 km/h. ¿Con qué velocidad ve pasar a esta persona, otra ubicada en el andén?

• Respuesta: v_A = 85 km/h

Problema nº 2

Cuando un tren pasa por una estación, un pasajero que viaja en sentado ve a un peatón correr en la misma dirección del tren, en sentido contrario. Si el tren posee una velocidad de 60 km/h y el peatón corre a 10 km/h. ¿Con qué velocidad el pasajero ve correr al peatón cuando pasa frente a él?

• Respuesta: v_T = 70 km/h

Problema nº 3

Un día muy ventoso la lluvia cae formando con la carretera un ángulo α = 30°. ¿Con qué velocidad se desplaza un automóvil cuyo conductor ve caer la lluvia con un ángulo β = 90°, si la velocidad de caída de la lluvia es de 8 m/s?

• Respuesta: v_A = 2,5 m/s

Problema nº 4

La lluvia cae verticalmente con una velocidad de 4 m/s. ¿Con qué ángulo la ve caer un ciclista que lleva una velocidad de 36 km/h?

• Respuesta: α = 21° 48'

Problema nº 5

Un avión vuela de A hacia B formando con su trayectoria un ángulo α = 45°, a una velocidad de 500 km/h respecto del aire. El viento sopla en dirección perpendicular a la trayectoria del avión. Calcular con qué velocidad sopla el viento.

• Respuesta: vᵥ = 353,55 km/h

Problema nº 6

¿Qué ángulo formará un avión que se dirige de A hacia B, si la velocidad del viento, que sopla perpendicular al segmento AB es de 120 km/h y la velocidad del avión respecto del aire es de 800 km/h?

• Respuesta: α = 8° 37'

Problema nº 7

Un río de un ancho D es cruzado en un tiempo t y por la corriente del río el bote amarra a una distancia e de su rumbo original. Determinar:

a) La velocidad del bote.

b) La velocidad del río.

• Respuesta:

a) v_b = 13,33 km/h;

b) vᵣ = 3,33 km/h

Problema nº 8

Para cruzar un río un barco tarda 40 minutos, si el río tiene una velocidad perpendicular a la del barco de 2 m/s, y entre el punto de salida y el de llegada se forma con la orilla de salida un ángulo α = 30°. Calcular:

a) La velocidad del barco.

b) El ancho del río.

c) La distancia entre el punto de partida y el de llegada respecto de la misma orilla.

• Respuesta:

a) v_b = 1,15 m/s;

b) l = 4.800 m; d = 2.771,28 m

Problema nº 9

Un bote va a cruzar un río de 10 metros de ancho, con una velocidad de 10 m/s hacia un punto que se encuentra frente al lugar de donde zarpa. El río fluye en forma perpendicular al bote con una velocidad de 5 m/s. Calcular:

a) ¿Cuánto tiempo tardó en cruzarlo?

b) ¿Qué distancia lo derivó el río?

• Respuesta:

a) t = 1 s;

b) e = 5 m

Problema nº 10

¿Qué ángulo α deberá formar el bote con la dirección AB para para poder mantener su rumbo perpendicular a la corriente del río si es de v_r = 0,5 m/s y la velocidad del bote es v_b = 3 m/s.

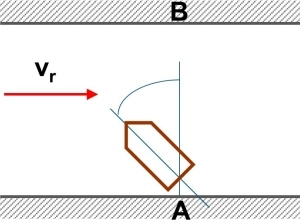
• Respuesta: α = 9° 35'

Bibliografía:

"Física". Hernán Miguel y Marcelo C. Cánepa. 1983. Argentina.

Autor: Ricardo Santiago Netto. Argentina