Dinámica de gases

Teorema general de la hidrodinámica aplicado a los gases

En hidrodinámica se postula el teorema general aplicado a los líquidos perfectos. En su demostración se supone la incompresibilidad del líquido, lo cual implica densidad constante, mientras no cambie la temperatura.

En los gases, se demuestra también el teorema general de la hidrodinámica suponiendo una masa de gas en movimiento estacionario; pero no es posible admitir la incompresibilidad, pues la densidad es función de la presión.

La ecuación de continuidad es la ecuación por la cual se establece que la masa de fluido no varía, es decir, que la masa que atraviesa una sección de filete (porción de conducto) es la misma que atraviesa cualquier otra sección del mismo filete y durante el mismo intervalo de tiempo. Esta ecuación, que en los líquidos adquiere forma sencilla, en los gases es bastante más compleja. Además, en el teorema general figura para los gases un término en que se vincula la variación de presión con la variación de volumen.

Sólo en el caso de suponer una circulación de gas a volumen constante podrá aplicarse la expresión del teorema de Bernoulli:

En la cual p es la presión hidrostática, ρ es el peso específico, v es la velocidad y h es la altura del punto considerado en la masa fluida, contada a partir de un plano horizontal de comparación.

Una experiencia curiosa que podemos explicar aplicando este teorema es la siguiente:

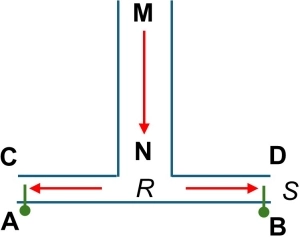
En el dispositivo de la figura, soplando fuertemente por el tubo MN. se observa que, contrariamente a lo que pudiera creerse, la placa AB móvil sube hasta tocar la CD.

La explicación es sencilla aceptando aplicable el teorema de Bernoulli. En efecto: como la sección de los filetes fluidos crece hacia la periferia, la velocidad de este disminuye, de acuerdo con la ecuación o ley de continuidad, teniéndose que la velocidad en el punto R es mayor que en el punto S. En el borde la presión hidrostática es igual a la presión exterior p₀ que actúa sobre la cara inferior de la placa AB. Aplicando el teorema de Bernoulli a dos puntos tales como R y S:

Como h_R = h_S y p_R = p₀, resulta:

Y como, además, dijimos que v_R > v_S, tendrá que ser:

p_R < p₀

Quiere decir que la presión que actúa en la cara superior de la placa AB es menor que la que actúa sobre la cara inferior. Habrá una fuerza resultante dirigida hacia arriba; cuando supere el peso, la placa se moverá.

Bibliografía:

"Física elemental". José S. Fernández y Ernesto E. Galloni. Argentina.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet).