Problema nº 10 de dinámica de los fluidos, sección de un orificio - TP03
Enunciado del ejercicio nº 10
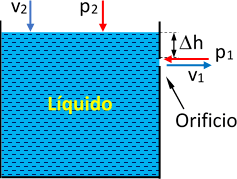
Por un orificio sale agua a razón de 180 l/min. Si se mantiene constante el desnivel de 30 cm entre el orificio y la superficie libre del líquido, ¿cuál es la sección del orificio?
Desarrollo
Datos:
Q = 180 l/min
Δh = 30 cm
g = 10 m/s²
Fórmulas:
Q = v·A
p₁ + ½·δ·v₁² + δ·g·h₁ = p₂ + ½·δ·v₂² + δ·g·h₂
Esquema:
Solución
Aplicamos la ecuación de Bernoulli para flujo ideal sin fricción.
p₁ + ½·δ·v₁² + δ·g·h₁ = p₂ + ½·δ·v₂² + δ·g·h₂
El enunciado dice "superficie libre del líquido" por lo tanto:
p₁ = p₂ = presión atmosférica
½·δ·v₁² + δ·g·h₁ = ½·δ·v₂² + δ·g·h₂
Y la velocidad en la superficie del líquido se considera nula:
v₂ = 0
½·δ·v₁² + δ·g·h₁ = δ·g·h₂
La densidad se simplifica:
½·v₁² + g·h₁ = g·h₂
Despejamos la velocidad:
½·v₁² = g·h₂ - g·h₁
½·v₁² = g·(h₂ - h₁)
Δh = h₂ - h₁
½·v₁² = g·Δh
v₁² = 2·g·Δh
![]()
Convertimos las unidades de caudal:
![]()
Convertimos las unidades de longitud:
Q = 0,003 m³/s
![]()
Δh = 0,3 m
Reemplazamos por los datos y calculamos:
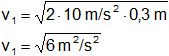
v₁ = 2,449489743 m/s
Con éste dato aplicamos la ecuación de continuidad:
Q = v·A
Despejamos "A":
![]()
Reemplazamos por los datos y calculamos:
![]()
A = 0,001224745 m²
Resultado, la sección de un orificio es:
A = 12,25 cm²
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP03
- | Siguiente ›
Ejemplo, cómo calcular la sección de un orificio