Problema nº 1 de dinámica de los fluidos, velocidad de salida - TP05

Enunciado del ejercicio nº 1

Se practica un orificio pequeño en la pared lateral de un recipiente lleno de líquido hasta un nivel de 80 cm más alto que el orificio. Calcular la velocidad teórica de salida.

Desarrollo

Datos:

Δh = 80 cm

g = 10 m/s²

Fórmulas:

p₁ + ½·δ·v₁² + δ·g·h₁ = p₂ + ½·δ·v₂² + δ·g·h₂

Esquema:

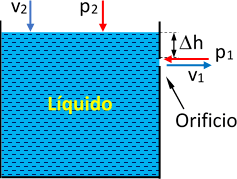
Solución

Aplicamos la ecuación de Bernoulli para flujo ideal sin fricción.

p₁ + ½·δ·v₁² + δ·g·h₁ = p₂ + ½·δ·v₂² + δ·g·h₂

El enunciado dice "superficie libre del líquido" por lo tanto:

p₁ = p₂ = presión atmosférica

½·δ·v₁² + δ·g·h₁ = ½·δ·v₂² + δ·g·h₂

Y la velocidad en la superficie del líquido se considera nula:

v₂ = 0

½·δ·v₁² + δ·g·h₁ = δ·g·h₂

La densidad se simplifica:

½·v₁² + g·h₁ = g·h₂

Despejamos la velocidad:

½·v₁² = g·h₂ - g·h₁

½·v₁² = g·(h₂ - h₁)

Δh = h₂ - h₁

½·v₁² = g·Δh

v₁² = 2·g·Δh

v₁ = √2·g·Δh

Convertimos las unidades:

Δh = 0,8 m

Reemplazamos y calculamos:

v₁ = √2·10 m/s²·0,8 m

v₁ = √16 m²/s²

v₁ = 4 m/s

Resultado, la velocidad de salida del líquido es:

v₁ = 4 m/s

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP05
• | Siguiente ›

Ejemplo, cómo calcular la velocidad de un de un flujo por un orificio