Problema nº 5 de dinámica de los fluidos, velocidad de salida - TP05

Enunciado del ejercicio nº 5

En el fondo de un tanque situado a 15 m de altura, se practica un orificio. ¿Con qué velocidad llega al suelo el agua que sale por él, si hay 75 cm de agua en el tanque y se supone que cae en el vacío?

Desarrollo

Datos:

h₁ = 75 cm

h₂ = 0 cm

Δh = 15 m

δ = 1.000 kg/m³

g = 10 m/s²

Fórmulas:

Q = v·A

p₁ + ½·δ·v₁² + δ·g·h₁ = p₂ + ½·δ·v₂² + δ·g·h₂

Esquema:

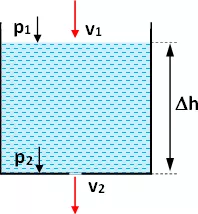
Solución

Para el tanque.

Aplicamos la ecuación de Bernoulli para flujo ideal sin fricción.

p₁ + ½·δ·v₁² + δ·g·h₁ = p₂ + ½·δ·v₂² + δ·g·h₂

Las presiones las podemos considerar iguales, las cancelamos:

p₁ = p₂

½·δ·v₁² + δ·g·h₁ = ½·δ·v₂² + δ·g·h₂

h₂ = 0 cm

½·δ·v₁² + δ·g·h₁ = ½·δ·v₂²

La velocidad en la superficie superior del tanque es despreciable:

v₁ = 0 m/s

δ·g·h₁ = ½·δ·v₂²

g·h₁ = ½·v₂²

Despejamos v₂:

v₂² = 2·g·h₁

Convertimos las unidades:

h₁ = 0,75 m

Reemplazamos por los valores:

v₂² = 2·10 m/s²·0,75 m

v₂² = 20 m²/s²·0,75

v₂² = 15 m²/s²

v₂ = √15 m²/s²

v₂ = 3,872983346 m/s

La v₂ es la velocidad inicial en el "tiro vertical" del agua del tanque hasta el piso.

De cinemática sabemos que:

vₛ² - v₂² = 2·g·Δh

Despejamos vₛ:

vₛ² = 2·g·Δh + v₂²

Reemplazamos por los valores calculamos:

vₛ² = 2·10 m/s²·15 m + 15 m²/s²

vₛ² = 300 m²/s² + 15 m²/s²

vₛ² = 315 m²/s²

vₛ = √315 m²/s²

vₛ = 17,74823935 m/s

Resultado, la velocidad del agua al llegar al suelo es:

vₛ = 17,75 m/s

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP05
• | Siguiente ›

Ejemplo, cómo calcular la velocidad de un de un flujo por un orificio