Problema nº 6 de dinámica de los fluidos, velocidad y caudal de una corriente estacionaria - TP05
Enunciado del ejercicio nº 6
Una tubería de 0,2 m de diámetro, llena de agua en movimiento, tiene un estrechamiento de 0,1 m de diámetro. Si la velocidad en la parte de 0,2 m es de 2 m/s, hallar:
a) La velocidad en el estrechamiento.
b) El caudal expresado en metros cúbicos por segundo.
Desarrollo
Datos:
v₁ = 2 m/s
d₁ = 0,2 m
d₂ = 0,1 m
Fórmulas:
Q = v₁·A₁ = v₂·A₂
A = π·(½·d)²
Esquema:
Solución
a)
Calculamos el área se la sección transversal:
A = π·¼·d²
Reemplazamos en la fórmula de caudal:
v₁·π·¼·d₁² = v₂·π·¼·d₂²
Simplificamos:
v₁·d₁² = v₂·d₂²
| v₂ = | v₁·d₁² |
| d₂² |
Reemplazamos por los valores y calculamos:
| v₂ = | 2 m/s·(0,2 m)² |
| (0,1 m)² |
| v₂ = | 2 m/s·0,04 m² |
| 0,01 m² |
| v₂ = | 0,08 m/s |
| 0,01 |
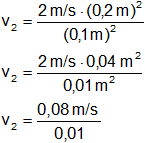
v₂ = 8 m/s
Resultado a), la velocidad en el estrechamiento es:
v₂ = 8 m/s
b)
Aplicamos la fórmula de caudal:
Q = v₁·A₁
Reemplazamos y calculamos:
Q = 2 m/s·π·¼·(0,2 m)²
Q = 2 m/s·π·¼·0,04 m²
Q = 0,0628 m³/s
Resultado b), el caudal es:
Q = 0,0628 m³/s
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP05
- | Siguiente ›
Ejemplo, cómo calcular la velocidad de una corriente estacionaria.