Problema nº 7 de dinámica de los fluidos, presión hidrostática - TP05

Enunciado del ejercicio nº 7

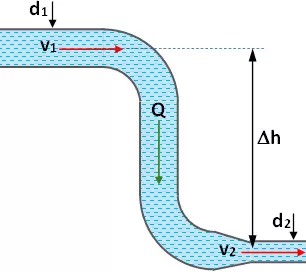
En determinado punto de una tubería la velocidad es de 1 m/s y la presión manométrica de 3·10⁵ Pa. Hallar la presión manométrica en un segundo punto de la línea situado 20 m por debajo del primero, si la sección transversal en él es la mitad que la del primero. El líquido de la tubería es agua.

Desarrollo

Datos:

p₁ = 3·10⁵ Pa

v₁ = 1 m/s

h₁ = 0 m

h₂ = -20 m

A₁ = 2·A₂

δ = 1.000 kg/m³

g = 10 m/s²

Fórmulas:

Q = v·A

p₁ + ½·δ·v₁² + δ·g·h₁ = p₂ + ½·δ·v₂² + δ·g·h₂

Esquema:

Esquema de una tubería con cambio de sección

Solución

Aplicamos la ecuación de Bernoulli para flujo ideal sin fricción.

p₁ + ½·δ·v₁² + δ·g·h₁ = p₂ + ½·δ·v₂² + δ·g·h₂

h₁ = 0 m

p₁ + ½·δ·v₁² = p₂ + ½·δ·v₂² + δ·g·h₂ (1)

De la ecuación de continuidad sabemos que:

Q = v₁·A₁ = v₂·A₂ = constante

v₁·A₁ = v₂·A₂

Y que:

A₁ = 2·A₂

Reemplazamos:

v₁·2·A₂ = v₂·A₂

Cancelamos:

v₁·2 = v₂

Reemplazamos en la ecuación (1):

p₁ + ½·δ·v₁² = p₂ + ½·δ·(2·v₁)² + δ·g·h₂

p₁ + ½·δ·v₁² = p₂ + ½·δ·4·v₁² + δ·g·h₂

p₁ + ½·δ·v₁² = p₂ + 2·δ·v₁² + δ·g·h₂

Despejamos p₂:

p₂ = p₁ + ½·δ·v₁² - (2·δ·v₁² + δ·g·h₂)

p₂ = p₁ + ½·δ·v₁² - 2·δ·v₁² - δ·g·h₂

p₂ = p₁ - 3·½·δ·v₁² - δ·g·h₂

Reemplazamos por los valores y calculamos:

p₂ = 3·10⁵ Pa - 3·½·1.000 kg/m³·(1 m/s)² - 1.000 kg/m³·10 m/s²·(-20 m)

p₂ = 3·10⁵ Pa - 3·500 kg/m³·1 m²/s² + 10.000 kg/m³·m/s²·20 m

p₂ = 3·10⁵ Pa - 0,015·10⁵ Pa + 2·10⁵ Pa

p₂ = 4,985·10⁵ Pa

Resultado, la presión manométrica en un segundo punto es:

p₂ = 4,985·10⁵ Pa

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular la presión hidrodinámica de una corriente estacionaria.