Campo gravitatorio: Concepto de campo
Concepto de campo
Diremos que en una región del espacio existe un campo creado por una magnitud física si es posible asignar en cada instante un valor a dicha magnitud para todos los puntos de dicha región.
Ejemplo:
Si tenemos un vaso que contiene agua con hielo, donde no se ha alcanzado el equilibrio térmico y medimos la T cada punto tendrá una T distinta. Existe un campo de T.
Si estudiamos la velocidad con la que se desplaza un fluido por una tubería vemos que depende del rozamiento de las paredes y la viscosidad, por tanto a cada pto de la tubería le corresponde una velocidad. Esto es un campo de velocidades.
Si la magnitud que define al campo es un escalar decimos que es un campo escalar (T) y si es vectorial que es un campo vectorial (velocidad).
Decimos que un campo es estacionario si no depende del tiempo.
Si la magnitud que define al campo permanece constante el campo es uniforme.
Un campo escalar se puede representar mediante superficies isoescalares, por ejemplo las superficies isobaras, que miden la presión atmosférica. El corte de estas superficies con planos paralelos a la superficie de la tierra definen las líneas isobaras.
Un campo vectorial se define mediante líneas de campo, que son líneas tangentes en cada punto a la magnitud vectorial que define el campo.
Cuando la magnitud que define el campo es una fuerza, se llaman campos de fuerzas.
Propiedades de las líneas de campo:
- Su sentido de recorrido y el vector que representa el campo coinciden en cada punto
- Pueden ser cerradas (campo magnético) o abiertas (campo gravitatorio y eléctrico)
- En cada punto de la línea el campo solo puede tener una dirección por lo que las líneas de campo no se pueden cortar
- Parten de manantiales o fuentes y llegan o convergen en sumideros
- Si el campo es uniforme, las líneas de campo son rectas paralelas
- En los puntos o zonas donde las líneas están más juntas o tienden a converger el campo es más intenso
Dos ejemplos de campos de fuerza son:
| Campos uniformes | Campos centrales |
| En ellos los vectores fuerza tienen el mismo módulo, dirección y sentido en todos los puntos del espacio. | En ellos las direcciones de todos los vectores fuerza convergen en un mismo punto, llamado centro del campo. El módulo del vector fuerza depende únicamente de la distancia del punto considerado al centro del campo. |
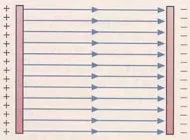 |  |
| Ejemplo: el campo eléctrico que existe entre las placas de un condensador plano. | Ejemplo: el campo gravitatorio de la Tierra. |
Campos conservativos. Energía potencial
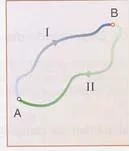
Un campo de fuerzas es conservativo si el trabajo que realizan las fuerzas del campo para trasladar una partícula de un punto A a uno B depende del punto inicial y final y no del camino seguido.
Propiedades
I) El trabajo que realiza el campo dentro de una trayectoria cerrada es cero.
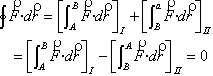
II) El trabajo que realiza el campo puede expresarse como la variación de la energía potencial entre dos puntos inicial y final.
![]()
W = EpA - EpB = -ΔEₚ
| W = ∫ | B | -m·g·dr |
| A |
W = -m·g·(hB - hA)
W = -m·g·hB + m·g·hA
W = -ΔEₚ
| W = ∫ | B | -k·x·dx |
| A |
W = -½·k·xB² + ½·k·xA²
W = -ΔEₚ
III) Teorema de la fuerzas vivas.
Supongamos un cuerpo que se desplaza con una trayectoria cualquiera bajo la acción de una fuerza F. (Supondremos que la F es paralela a la dirección de desplazamiento, si no habría que coger únicamente su componente tangencial). El trabajo realizado por F es:
![]()
| W = ∫ | B | F·dr |
| A |
| W = ∫ | B | -m·a·dr |
| A |
| W = ∫ | B | -m· | dv dt | ·dr |
| A |
| W = ∫ | B | m·v·dv |
| A |
| W = m·½·[v²] | B |
| A |
W = ½·m·vB² - ½·m·vA²
Esto se conoce como "teorema de las fuerzas vivas". Sea cual sea la naturaleza de las fuerzas que actúan sobre un cuerpo, el trabajo total realizado al trasladarlo entre dos puntos es igual a la variación de la energía cinética. W = ΔEc.
Debemos recordar, por tanto que si sobre un cuerpo solo actúan fuerzas conservativas su energía mecánica se mantiene constante.
W = ΔEc
W = -ΔEₚ
Por tanto EcB - EcA = EpA - EpB
Por tanto EcB + EpB = EpA + EcB
Son campos conservativos cualquier central, el eléctrico, el gravitatorio y el elástico.
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).