Campo gravitatorio: Dinámica de rotación

Dinámica de rotación

Momento de un vector respecto de un punto

Consideraremos que el vector es una fuerza.

El momento de una fuerza F aplicada en el punto P, con respecto a un punto O, es un vector con las siguientes características:

• Módulo: El producto de la fuerza por la distancia del punto a la línea de acción de la fuerza
• Dirección: La de la perpendicular la plano formado por el punto y la línea de acción de la fuerza
• Sentido: el del avance de un sacacorchos al llevar r sobre F por el camino más corto

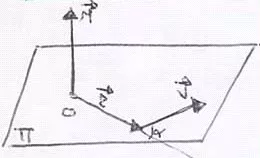	Esto es un producto vectorial M = r×F Propiedades. Las del producto vectorial. Y una más:
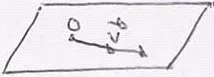	Si la recta direccional del vector pasa por el centro de momentos el vector es nulo, no hay momento. |M| = v·d d = 0 |M| = 0

Todo esto es muy útil, por ejemplo en aplicaciones como la ley de la palanca. Esta ley establece que el efecto de una fuerza al actuar sobre un punto de aplicación no depende solo de su valor, sino también de la distancia al punto de apoyo, o eje de giro. Aparece una nueva magnitud que es el producto de una fuerza por una distancia, lo llamamos momento.

Momento cinético o angular

Momento cinético o angular de una partícula de masa m, que se mueve con velocidad v, con respecto a un punto O es el producto vectorial de su posición, r por su cantidad de movimiento, p.

L = r×p = r×m·p

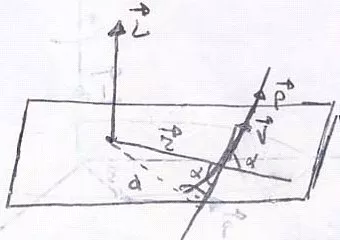
L = r·(sen α) = p·d

sen α = d/r

d = r·(sen α)

Teorema del momento angular

Derivando la ecuación anterior se obtiene:

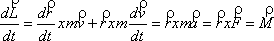
Ya que la derivada del vector de posición respecto del tiempo es la velocidad y el producto vectorial de esta por la cantidad de movimiento es cero, pues son vectores paralelos.

Conservación del momento angular. Consecuencias

Si el momento angular M = 0 entonces L = constante. Es decir, si la suma de los momentos de las fuerzas exteriores que actúan sobre un sistema es cero, el momento angular del sistema permanece constante.

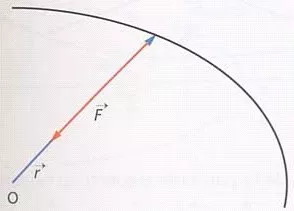
Por ejemplo esto ocurre en el caso de las fuerzas centrales ya que al tener r y F la misma dirección el momento es cero.

El momento de una fuerza central respecto al centro O polo de atracción es nulo

Par de fuerzas

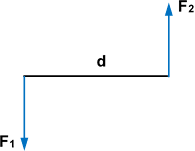
Se denomina par de fuerzas a dos fuerzas paralelas, iguales en módulo y de sentido contrario. La resultante es 0. R = F₁ - F₂ = 0.

No produce movimiento de traslación, solo de rotación El módulo del producto de un par de fuerzas es igual al producto del módulo de una de las fuerzas por la distancia entre ellas. M = F·d. A d se le conoce como brazo del par

• Fuente:

Física de 2° de Bachillerato - Colegio Montpellier

Autor: Leandro Bautista. España.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet).

• ‹ Anterior
• |
• Siguiente ›