Campo gravitatorio: Leyes de Kepler
Leyes de Kepler
A finales del siglo XVI, un astrónomo danés, Brahe, calculó numerosos datos sobre el movimiento de los planetas con muchísima precisión. También trató de medir algún paralaje pero no lo consiguió. Conocía las teorías de Nicolás Copérnico, pero también el poder de la iglesia y creó un modelo geocéntrico y heliocéntrico a la vez. Todos los planetas giraban alrededor del Sol y todo ese conjunto, a su vez, gira alrededor de la Tierra que está inmóvil en el centro del universo.
Johannes Kepler fue su discípulo, pero era un Coperniciano convencido. A la muerte de Brahe, Kepler decidió interpretar esos datos adaptándolos a las órbitas circulares de Copérnico. Los cálculo cuadraban hasta Marte. Según los datos de Brahe la orbita de Marte estaba a 8' de arco (0, 13°) fuera del esquema de Copérnico. Al estudiar esta discrepancia Kepler se dio cuenta de que si las órbitas son elípticas en las que en uno de los focos se situaba el Sol se solucionaba el problema.
Con esto y el resto de los datos Kepler enunció tres leyes que describían el movimiento planetario:
1° ley de Kepler: Los planetas describen órbitas elípticas en uno de cuyos focos está el Sol.
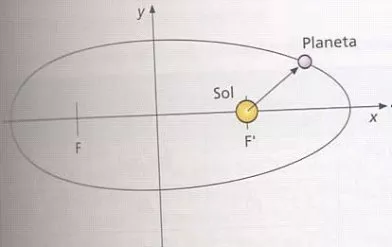
Primera ley de Kepler (ley de las órbitas)
2° ley de Kepler:
S₁/t₁ = S₂/t₂ = constante.
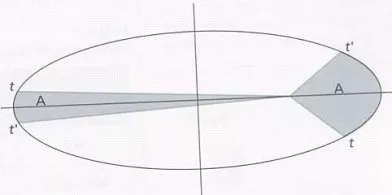
Segunda ley de Kepler (ley de las áreas)
Velocidad areolar: Es el cociente entre el área barrida y el tiempo empleado en barrerla. Vₐ = s/t m/s. Por esto a esta propiedad también se conoce como "teorema de las áreas".
Esta propiedad es consecuencia del "teorema de conservación del momento angular". Como el sistema solar es un sistema aislado ∑M = 0 y por tanto L = constante. Como las fuerzas de atracción son centrales F y r son paralelos y por tanto M = 0. Las órbitas son planas ya que si L = constante lo es en dirección y sentido, L es perpendicular a r y a v y por tanto deben estar en un mismo plano.
Por tanto:
L = m·v·r
| L = r·m· | ds | = r·m· | r·dθ | = r²·m· | dθ |
| dt | dt | dt |
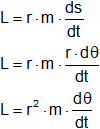
Como sabemos que:
| π·r²·θ | ||||||
| dA | = | 2·π | = | r² | · | dθ |
| dt | dt | 2 | dt | |||
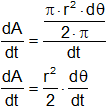
Despejando:
| dθ | = | 2 | · | dA |
| dt | r² | dt |
Sustituyendo arriba:
| L = r²·m· | 2 | · | dA | = 2·m· | dA |
| r² | dt | dt |
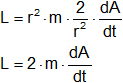
Así que si L = constante ⟶ dA/dt = constante.
Como consecuencia de esta 2° ley de Kepler: las áreas barridas en tiempos iguales son iguales.
t₁ = t₂ ⟶ S₁/t₁ = S₂/t₂ ⟶ S₁ = S₂
Nota: Perihelio Posición de un planeta en su órbita más próxima al Sol. Afelio: Posición más alejada. Si hablamos de órbita alrededor de la Tierra se llama apogeo y perigeo
Esto quiere decir que en los puntos próximos al perihelio la v es mayor que en el afelio ya que recorre más arco en el mismo t.
3° ley de Kepler: Los cuadrados de los períodos son directamente proporcionales a los cubos de los semiejes mayores (distancia media) de las elipses.
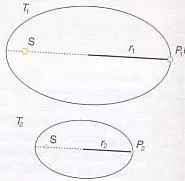 | T₁²/r₁³ = T₂²/r₂³ = T₃²/r₃³ = … = cte |
Período es el tiempo que tarda un planeta en dar una vuelta completa.
Las leyes de Kepler son válidas para el movimiento de los planetas alrededor del Sol y de los satélites alrededor del planeta.
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
Dinámica física ejemplos