Campo gravitatorio: Nociones actuales sobre el sistema solar
Nociones actuales sobre el sistema solar
La idea que tenemos hoy acerca del sistema solar no coincide con mucho de lo visto hasta ahora. Para empezar, tampoco el Sol es centro de nada. Nuestro sistema planetario no es más que uno de los muchos que posiblemente acompañan a numerosas estrellas de la galaxia en que habitamos, la Vía Láctea. A su vez nuestra galaxia no es más que una de los billones o trillones de galaxias que posiblemente componen el Universo.
Características de nuestro sistema solar:
- Todos los planetas efectúan dos movimientos distintos: uno de traslación alrededor del Sol y otro de rotación en torno a su propio eje
- Todos los planetas describen orbitas planas alrededor del Sol.-
- Casi todas las órbitas planetarias están aproximadamente en el mismo plano
- Todos los planetas se trasladan en el mismo sentido alrededor del Sol (en sentido antihorario). La mayoría de los satélites hacen lo mismo alrededor de los planetas
- El eje de rotación de la mayor parte de los planetas (salvo Urano y Plutón) es prácticamente perpendicular al plano orbital
- La mayoría de los satélites describen órbitas en el plano ecuatorial delos planetas. (Salvo los de Urano y Plutón)
- Todos los planetas rotan en sentido antihorario excepto Venus, Urano y Plutón
- La fuerza que gobierna el movimiento planetario es de tipo central y actúa en la dirección que une planeta y Sol
- Las órbitas planetarias son estables. Asumiendo que la masa del planeta apenas varía, su distancia media al Sol permanece constante
- Las orbitas de los satélites en torno a los planetas son planas y estables
- La fuerza que gobierna el movimiento de los satélites en torno a los planetas es de tipo central, dirigida a lo largo de la línea que une satélite y planeta
Ejemplo de aplicación
Deduce cuál es la relación entre las velocidades del planeta en los puntos A y B de la figura en función de las distancias rA y rB de esos puntos al Sol. ¿Avalan estos resultados las observaciones de Kepler?
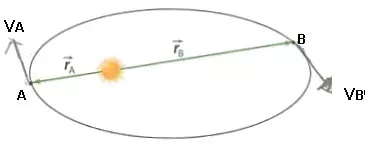
El valor del momento angular del planeta con respecto al Sol en el punto A viene dado por:
LA = rA·m·vA·sen 90° = rA·m·vA
Donde m es la masa del planeta.
En el punto B, el valor del momento angular es:
LB = rB·m·vB·sen 90° = rB·m·vB
Puesto que la fuerza es central, el momento angular permanece constante, con lo que:
LA = LB ⇒ rA·vA = rB·vB ⇒ vA/vB = rB/rA
Es decir, la relación entre las velocidades es inversa a la relación entre las distancias, lo que significa que cuanto mayor sea la distancia, menor será la velocidad, resultado que concuerda con lo expuesto por Johannes Kepler en su segunda ley.
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).