Campo gravitatorio terrestre
Llamaremos campo gravitatorio a la perturbación que un cuerpo produce en el espacio que le rodea por el hecho de tener masa.
Podemos considerar una partícula de masa M que perturba el espacio que le rodea, creando un campo gravitatorio. Dicho campo se hace evidente cuando una partícula testigo de masa m se sitúa en él a una distancia r del centro de M y es atraída con una fuerza:
![]()
Donde:
r = R + d
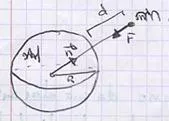
Estaremos fuera del campo gravitatorio cuando F = 0. Para ello r debe ser ∞. Esto es teórico. Si las masas son pequeñas en relación a la distancia la F ⟶ 0. Ejemplo: tiza-bolígrafo
Intensidad del campo gravitatorio
La fuerza depende de la cantidad de masa m. Vamos a definir una característica del campo que solo dependa de la masa que origina el campo M y la distancia al punto que consideremos.
La intensidad del campo gravitatorio, g,
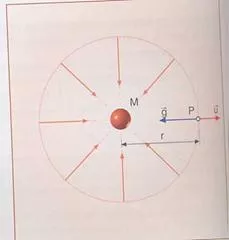
Para determinar el campo gravitatorio creado por una masa puntual M situamos una masa de prueba m en un punto P del espacio a una distancia R de la masa M. Calculamos la F por unidad de masa.
![]()
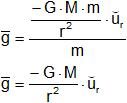
Podemos decir que el campo gravitatorio tiene las siguientes propiedades:
- Es un campo central y disminuye con el cuadrado de la distancia
- El signo negativo es porque g y ūᵣ tienen sentidos contrarios. Las fuerzas gravitatorias siempre son atractivas
Podemos escribir la ecuación de la intensidad como F = m·g.
Esto coincide con P = m·g.
En la superficie de la Tierra:
![]()
El campo gravitatorio se visualiza a través de unas líneas imaginarias que se llaman líneas de fuerza. Son la trayectoria que seguiría la unidad de masa dejada en libertad dentro del campo gravitatorio.
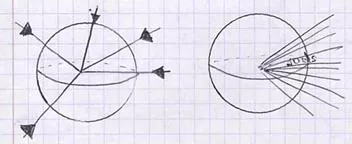
Así también puede definir la intensidad de campo.
uds unidad de superficie.
Intensidad de campo es el número de líneas que atraviesan la uds colocada perpendicularmente a dichas líneas
Si suponemos que la causante está en el infinito con respecto al observador:

- Pueden considerarse las líneas paralelas en el cilindro
- IA = IB
Flujo del campo gravitatorio (Φ)
Es el número de líneas que atraviesan una región del espacio.
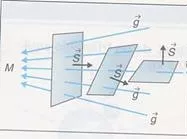
Tenemos un campo gravitatorio g, que atraviesa una superficie S, que podemos caracterizar por un vector S, perpendicular a la superficie y de módulo su área (Esto es la interpretación geométrica del producto vectorial).
Se define el Φ del campo gravitatorio como:
Φ = g·S = g·s·cos θ
Si g y S son perpendiculares no hay flujo.
Teorema de Gauss
Gauss definió un Teorema para calcular el flujo del campo electrostático. Para el campo gravitatorio se usa una modificación de este.
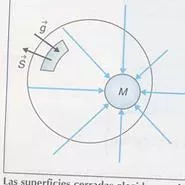
Sea M una masa puntual encerrada en una esfera de radio r.
El flujo es Φ = g·S = g·s·cos 180° = -g·S
Si M está en el centro de la esfera:
![]()
Como S = 4·π·r² ⟶ Φ = -G·(M/r²)·4·π·r² = -4·π·G·M
M es la masa encerrada dentro de la superficie
"El flujo del campo gravitatorio a través de una superficie cerrada es el producto de una constante (- 4·π·G) por la masa encerrada dentro de la superficie".
Mediante el Teorema de Gauss puede justificarse que una esfera homogénea se comporte en su exterior como una masa puntual situada en su centro. Basta con elegir una esfera concéntrica de radio r y suponer que el campo gravitatorio es constante y perpendicular a la superficie de la esfera elegida.
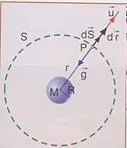
Teorema de Gauss
Φ = -4·π·G·Minterior
Definición de Φ:
Φ = -g·S = -g·4·π·r²
Igualando:
![]()
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
Dinámica física ejemplos