Campo gravitatorio: Energía potencial de un campo gravitatorio
Vamos a intentar calcular el W para llevar una masa m desde un punto a otro dentro del campo gravitatorio. Es un campo conservativo central
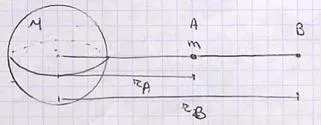
Nota:
| ∫ | 1 r² | ·dr = ∫ r⁻²·dr = | r⁻² ⁺ ¹ -2 + 1 | = | r⁻¹ -1 | = | -1 r |
| WAB = ∫ | B | F·dr |
| A |
| WAB = ∫ | B | F·cos 180°·dr |
| A |
| WAB = -∫ | B | F·dr |
| A |
| WAB = -∫ | B | G· | M·m r² | ·dr |
| A |
| WAB = -∫ | rB | G· | M·m rr | ·dr |
| rA |
| WAB = -G·M·m·(- | 1 r | ) | rB |
| rA |
| WAB = -G·M·m·( | 1 rA | - | 1 rB | ) |
Es el trabajo que se realiza para llevar la masa m del punto A al B dentro del campo gravitatorio.
Sabemos que:
W = -ΔEₚ = EpA - EpB
| EpA - EpB = -G·M·m·( | 1 rA | - | 1 rB | ) |
Es la variación de la Eₚ que ha sufrido el cuerpo cuando ha pasado del punto A al B
Para obtener la Eₚ relativa a un punto del campo hay que fijar un sistema de referencia que asigne 0 al valor de la Eₚ.
Se elige el ∞. Si llevo B al infinito rB = ∞ ⟶ 1/rB = 0
EpA = -G·M/rA Trabajo que hay que realizar para llevar la masa desde A al ∞ y al revés (desde ∞ al punto A). También expresa la Eₚ de la masa m en el punto A.
W > 0 si:
- La masa se desplaza por acción de las fuerzas del campo gravitatorio
- La masa m disminuye su energía potencial gravitatoria
- Se acercan dos masas
W < 0 si:
- La masa m se desplaza por acción de una fuerza exterior al campo gravitatorio
- La masa m aumenta su energía potencial gravitatoria
- Se separan dos masas
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
Dinámica física ejemplos