Potencial en el campo gravitatorio
Los campos de fuerza conservativos se pueden caracterizar además de por su intensidad por una magnitud escalar, el potencial. El potencial gravitatorio se define como la energía potencial por unidad de masa colocada en un punto.
![]()
Se identifica con el trabajo que es preciso realizar contra las fuerzas del campo, para trasladar una masa de 1 kg desde A hasta el infinito.
En un punto B sería:
![]()
y por tanto:
![]()
Diferencia de potencial entre dos puntos. Es igual al trabajo que hay que realizar para llevar la unidad de masa de un punto a otro.
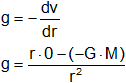
![]()
Representación del campo gravitatorio
El campo gravitatorio puede representarse mediante superficies equipotenciales que son el conjunto de puntos del campo que están al mismo potencial.
El trabajo realizado para trasladar una masa cualquiera m entre dos puntos A y B de una superficie equipotencial será nulo.
WAB = -ΔEₚ = EpA - EpB = m·(VA - VB) = m·0 = 0
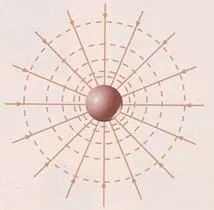
g corta a la superficie equipotencial perpendicularmente en cada punto.
WAB = 0
∫F·dř = 0
F y dr son perpendiculares.
F y g llevan la misma dirección y dr entre dos puntos A y B es tangente a la superficie ⟶ g es perpendicular a la superficie
Energía potencial en la Tierra
Si la masa creadora del campo es la masa de la Tierra (MT) la energía potencial será:
![]()
Si elegimos como Eₚ = 0 el suelo de la Tierra rB = RT ⟶ EpB = 0
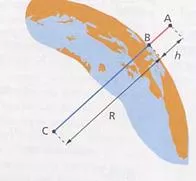
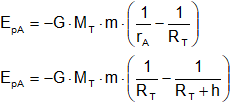
Operando y sabiendo que:
![]()
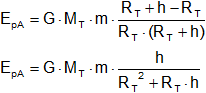
Si h << << < RT
G·MT·m·h/R² y por tanto
EpA = g₀·m·h = m·g₀·h. Valido para pequeñas alturas sobre la superficie de la Tierra.
¿A qué altura sobre la superficie de la Tierra el valor de g es la ¼ parte del de la superficie?
![]()
g = ¼·g₀
4·g = g₀
![]()
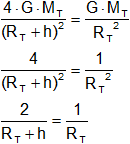
2·RT = RT + h
RT = h
Calcula el potencial gravitatorio y compáralo con el de la superficie.
![]()
![]()
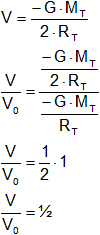
V₀ = 2·V
V = ½·V₀
¿Qué relación existe entre las energías potenciales de un cuerpo de masa m?
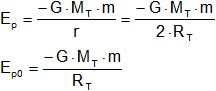
Planteando la relación:
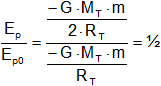
Eₚ = ½·Eₚ₀
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).