Movimiento de planetas y satélites
Velocidad orbital de un satélite
Supongamos que hay una partícula de masa m con trayectoria alrededor de la tierra circular de radio r.
Suponemos que la Tierra está quieta, m lleva velocidad v y no gasta combustible.
![]()
• Nota: La ac no depende de la masa, otro cuerpo de masa m' tendría la misma.

Todas las masas en la misma órbita tienen la misma velocidad lineal.
La fuerza gravitatoria de atracción de la Tierra es:
![]()
Es la misma fuerza vista desde dos puntos de vista distintos.
![]()
![]()
Por tanto
![]()
Energía Total

Se llama energía total a la que tiene una masa o satélite que órbita alrededor de la tierra.
Es la suma de la Ec y de la Eₚ
![]()
Ec = ½·m·v²
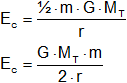
La energía total es la suma de las dos energías:
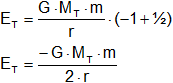
Esta es la energía necesaria para que un satélite esté en órbita.
Es negativa e igual a la mitad del valor de la energía potencial. El signo menos corresponde a orbitas cerradas de objetos que no tienen energía suficiente para escapar de la atracción terrestre.
Cuando un satélite cambia de órbita en ausencia de fuerzas exteriores su Energía mecánica se conserva.
EcA + EpA = EcB + EpB
Entonces si lanzamos el satélite desde la superficie de la tierra ya tiene una cierta energía potencial
Ec0 + Eₚₒ = Ecf + Epf
![]()
Por tanto:
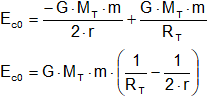
Esto se conoce como energía de satelización.
Si queremos calcular la velocidad inicial necesaria para llegar a esa órbita.
![]()
Por tanto:
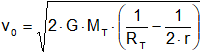
Velocidad de escape
Es la velocidad que hay que comunicar a un cuerpo de masa m situado sobre la superficie del planeta para que pueda escapar del campo gravitatorio e irse al ∞.
En el ∞ la EM = 0 ya que hemos dicho que la Eₚ = 0 y la velocidad con la que llega es 0, por tanto Ec + Eₚ = 0.
Por tanto:
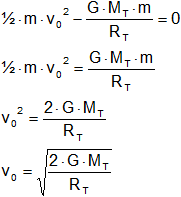
Se puede escribir:
![]()
![]()
Satélites geoestacionarios
Un satélite se llama geoestacionario cuando se encuentra siempre sobre el mismo punto de la superficie terrestre, es decir, recorre toda su orbita en el tiempo que la tierra hace una rotación completa (24 h)
Aplicando la 3° ley de Kepler:
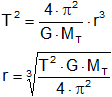
Si sustituimos los datos:
T = 24 h = 86.400 s
G = 6,67·10⁻¹¹ N·m²/kg² el valor de r = 4,2·10⁷ m
MT = 5,97·10²⁴ kg
También puede calcularse r igualando la Fc a la fuerza de Newton m·ω²·r = G·M·m/r² y despejar "r"
Como RT = 6.370·10³ m ⟶ h = r - RT = 35.863. Altura de la órbita.
Son órbitas de altitudes elevadas y no obtienen imágenes de alta resolución de la Tierra. Son órbitas ecuatoriales y se usan para aplicaciones meteorológicas y de comunicaciones. Las órbitas de baja altitud (600 a 1.200 km) se llaman heliosincronas (orientación fija respecto al Sol). Se usan para observación de la Tierra.
Razona:
- Si el cero de energía potencial gravitatoria de una partícula de masa m se sitúa en la superficie de la Tierra ¿Cuál es le valor de la energía potencial de la partícula cuando se encuentra a una distancia ∞ de la Tierra?
La energía potencial de una masa m a una distancia r de la Tierra es Eₚ = -G·MT·m/r. Esta es nula cuando r ⟶ ∞. La Eₚ siempre es negativa y tiende a 0 cuando la r ⟶ ∞. En la superficie será -G·M·m/RT
Si cambiara el origen y tomamos la superficie de la Tierra en el ∞ será E = G·M·m/RT
- ¿Puede ser negativo el trabajo de una fuerza gravitatoria? ¿Y su energía potencial?
La Eₚ si, como hemos visto, ya que depende del origen.
El trabajo no, ya que la fuerza gravitatoria hace un W espontáneo y positivo.
No influye el origen ya que es una variación de la energía y es independiente del origen
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
Dinámica física ejemplos