Ejemplo n° 1 de las leyes de Kepler

Ejemplo nº 1

Calcula el período de revolución de Marte sabiendo que la distancia media de Marte al Sol es de 228 millones de km, la distancia media de la Tierra al Sol de 149,6 millones de km y el período de revolución de la tierra de 365,26 días.

Desarrollo

Datos:

r_M = 228.000.000 km

r_T = 149.600.000 km

T_T = 365,26 días

Fórmulas:

Solución

Despejamos T_M:

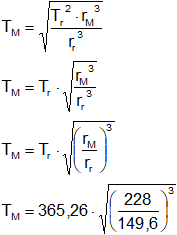
T_M = 687,23 días

Resultado, el período de revolución de Marte es:

T_M = 687,23 días

Ejemplo nº 2

El período de traslación de un planeta es 12 veces mayor que el período de traslación de la Tierra alrededor del Sol. Halla la distancia del Sol a ese planeta si la distancia Tierra - Sol es de 149.500.000 km

Desarrollo

Datos:

T_F = 12·T_T

r_T = 149.500.000 km

Fórmulas:

Solución

Reemplazamos por los valores y calculamos:

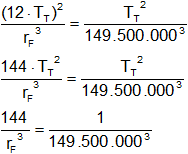
r_F³ = 144·(149,5·10⁵)³

Resultado, la distancia del Sol al planeta es:

r_F = 7,836·10⁸ km

Ejemplo nº 3

Si el radio de la orbita circular de un planeta A es cuatro veces mayor que el de otro B ¿en qué relación están su períodos y sus velocidades medias?

Desarrollo

Datos:

r_A = 4·r_B

Fórmulas:

v = 2·π·r/T

Solución

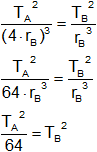
T_A² = 64·T_B²

T_A = 8·T_B

Resultado, la relación entre sus períodos es:

T_A = 8·T_B

La velocidad v = s/t = 2·π·r/T

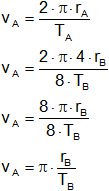
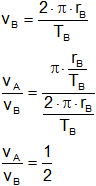
Resultado, la relación entre sus velocidades medias es:

v_B = 2·v_A

‹‹ Regresar al apunte: AP06

• Fuente:

Física de 2° de Bachillerato - Colegio Montpellier

Autor: Leandro Bautista. España.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet).

Ejemplo, cómo calcular el periodo de revolución