Problema nº 8 de dinámica, trayectoria de un cuerpo - TP01
Enunciado del ejercicio nº 8
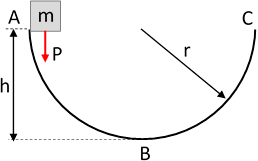
Un cuerpo de masa "m", se suelta en el punto más alto de una superficie semiesférica de 3 m de radio, y resbala sin rozamiento. Determinar el punto en el cual la masa deja de tener contacto con la superficie.
Desarrollo
Datos:
r = 3 m
V₀ = 0 m/s
g = 10 m/s²
Fórmulas:
P = m·g
Esquema:
Solución
Entre la superficie y el cuerpo no hay rozamiento, por lo tanto, el movimiento estará afectado únicamente por la aceleración de la gravedad (g) sin importar la masa "m".
Este tipo de casos se puede resolver sencillamente con el teorema de la variación de la energía mecánica, luego lo veremos.
Por el momento lo resolveremos con ecuaciones de cinemática, se trata de un movimiento uniformemente variado.
El trayecto de "A" hasta "B" se puede considerar caída libre.
El trayecto de "B" hasta "C" se puede considerar tiro vertical hacia arriba.
Entonce:
r = h = 3 m
Se desconoce el tiempo, por lo tanto, sólo usaremos la ecuación (3).
vf = v₀ + g·t (1)
y = v₀·t + ½·g·t² (2)
vf² - v₀² = 2·g·h (3)
Tramo AB (caída libre):
vfB² - v₀² = 2·g·h
g > 0
V₀ = 0 m/s
Reemplazamos por los datos y calculamos:
vfB² = 2·10 m/s²·3 m
vfB² = 60 m²/s²
Lo dejamos expresado así, es el cuadrado de la velocidad en el punto más bajo.
Tramo BC (tiro vertical):
En este tramo utilizará la velocidad hallada anteriormente para subir.
vfC² - v0B² = 2·g·h
v0B² = vfB² = 60 m²/s²
g < 0
Reemplazamos por los datos y calculamos:
vfC² = 60 m²/s² + 2·(-10 m/s²)·3 m
vfC² = 60 m²/s² - 60 m²/s²
vfC² = 0 m²/s²
vfC = 0 m/s
Como vemos en el punto "C" la velocidad se anula, significa que alcanza la altura máxima a los 3 m.
Resultado, el punto en el que la masa deja de tener contacto con la superficie es:
h = 3 m
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP01
- | Siguiente ›
Ejemplo, cómo calcular la trayectoria de un cuerpo