Problema nº 5 de dinámica, fuerza de vínculo y aceleración de un cuerpo - TP02

Enunciado del ejercicio nº 5

En el sistema de la figura, la fuerza aplicada a la cuerda AB es de 40 N, el cuerpo pesa 50 N. Despreciando el rozamiento, determinar:

a) El módulo de la fuerza de vínculo (reacción del plano).

b) El módulo de la aceleración del cuerpo puntual.

Desarrollo

Datos:

P = 50 N

F_AB = 40 N

α = 37°

Se adopta g = 10 m/s²

Fórmulas:

P = m·g

F = m·a

Condición de equilibrio (Primera ley de Newton):

∑Fₓ = 0

∑F_y = 0

∑MF = 0

Esquema:

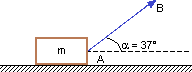
Solución

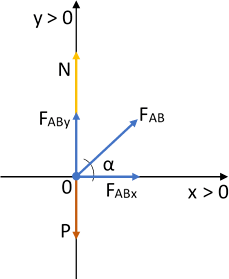
Diagrama de fuerzas

Según las condiciones de equilibrio y de acuerdo con el diagrama tenemos que, en el eje X:

F_ABx = m·a (no está en equilibrio)

En el eje Y:

N + F_ABy - P = 0

También sabemos que:

F_ABy = F_AB·sen α

F_ABx = F_AB·cos α

a)

De la segunda ecuación despejamos "N":

N = -F_ABy + P

Reemplazamos por los datos y calculamos:

N = -F_AB·sen α + P

N = -40 N·sen 37° + 50 N

N = -40 N·0,602 + 50 N

N = -24,07 N + 50 N

Resultado, la reacción del plano es:

N = 25,93 N

b)

El cuerpo está en movimiento y posee aceleración, aplicamos la ecuación del eje "X":

F_ABx = m·a

Reemplazamos por los datos y calculamos:

F_AB·cos α = m·a

La masa la hallamos a partir de la fuerza peso:

Despejamos "a":

Reemplazamos por los valores y calculamos:

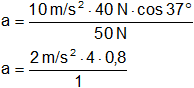
Resultado, la aceleración del cuerpo es:

a = 6,39 m/s²

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP02
• | Siguiente ›

Ejemplo, cómo calcular la fuerza de vínculo y la aceleración de un cuerpo