Problema nº 6 de dinámica, aceleración de un sistema de masas en un plano inclinado - TP02

Enunciado del ejercicio nº 6

Un cuerpo de masa m = 60 kg esta apoyado sobre un plano de inclinación 37°, como muestra la figura. La intensidad de la fuerza "F" que ejerce la soga "AB" es de 500 N. Despreciando el rozamiento, calcular el módulo de la aceleración del bloque.

Desarrollo

Datos:

m = 60 kg

F_AB = 500 N

α = 37°

β = 37°

Se adopta g = 10 m/s²

Fórmulas:

P = m·g

F = m·a

Condición de equilibrio (Primera ley de Newton):

∑Fₓ = 0

∑F_y = 0

∑MF = 0

Esquema:

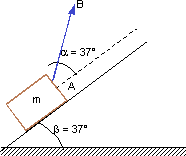
Solución

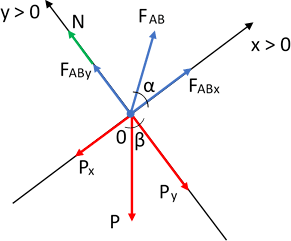
Diagrama de fuerzas

Según el enunciado y las condiciones de equilibrio y, de acuerdo con el diagrama tenemos que, en el eje X:

F_ABx - Pₓ = m·a (no está en equilibrio)

En el eje Y:

N + F_ABy - P_y = 0

También sabemos que:

F_ABy = F_AB·sen α

F_ABx = F_AB·cos α

y

Pₓ = P·sen β

P_y = P·cos β

Empleamos la primera ecuación de equilibrio (eje X):

F_ABx - Pₓ = m·a

Reemplazamos por las componentes:

F_AB·cos α - P·sen β = m·a

Despejamos "a":

Como P = m·g:

Reemplazamos por los datos y calculamos:

Resultado, la aceleración del bloque es:

a = 0,637 m/s²

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP02
• | Siguiente ›

Ejemplo, cómo calcular la aceleración de un sistema de masas en un plano inclinado