Problema nº 8 de dinámica, fuerza resultante de un sistema de masas en movimiento - TP02
Enunciado del ejercicio nº 8
¿Cuál es la fuerza total que actúa sobre un pasajero de 60 kg de masa que está en el asiento de un automóvil, que acelera a razón de 8,3 m/s²?
Desarrollo
Datos:
m = 60 kg
a = 8,3 m/s²
g = 10 m/s²
Fórmulas:
F = m·a
Condición de equilibrio (Primera ley de Newton):
∑Fₓ = 0
∑Fy = 0
∑MF = 0
h² = a² + b²
Solución
Realizamos el diagrama de fuerzas:
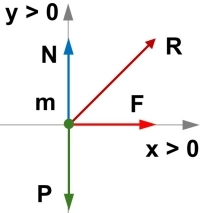
Planteamos las ecuaciones en cada eje.
En el eje X:
F = m·a
En el eje Y:
N - P = 0
La normal al vínculo (N) se equilibra con la fuerza peso (P).
N = P
La fuerza que recibe el pasajero es la del asiento, que son F y N, que son las componentes de la fuerza total o resultante.
Resolvemos mediante el Teorema de Pitágoras:
h² = a² + b²
R² = F² + N²
R² = (m·a)² + (m·g)²
Reemplazamos por los datos y calculamos:
R² = (60 kg·8,3 m/s²)² + (60 kg·10 m/s²)²
R² = (498 N)² + (600 N)²
R² = 248.004 N² + 360.000 N²
R² = 608.004 N²
![]()
R = 779,7461125 N
Resultado, la fuerza total que actúa sobre el pasajero es:
R = 780 N
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP02
- | Siguiente ›
Ejemplo, cómo calcular la fuerza resultante de un sistema de masas en movimiento