Problema nº 1 de dinámica con rozamiento, fuerza resultante de un sistema de masas en movimiento - TP03
Enunciado del ejercicio nº 1
Una caja que pesa 200 N es arrastrada por una cuerda que forma un ángulo α con la horizontal, según muestra la figura. El coeficiente de rozamiento estático entre la caja y el suelo es μₑ = 0,6. Si la caja se encuentra inicialmente en reposo, calcular la fuerza mínima para ponerla en movimiento. Resolver el problema para:
a) α = 30°.
b) α = 0°.
Desarrollo
Datos:
P = 200 N
μₑ = 0,6
V₀ = 0 m/s
Se adopta g = 10 m/s²
Fórmulas:
P = m·g
F = m·a
Fᵣ = μₑ·N
Condición de equilibrio (Primera ley de Newton):
∑Fₓ = 0
∑Fy = 0
∑MF = 0
Esquema:
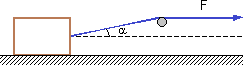
Solución
La fuerza actúa por una cuerda supuesta inextensible, por lo tanto, su acción es directa.
a)
Para α = 30°:
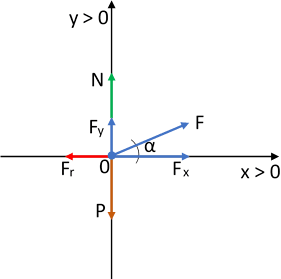
Diagrama de fuerzas
En el eje X:
Fₓ - Fᵣ = 0 (1)
En el eje Y:
N + Fy - P = 0 (2)
También sabemos que:
![]()
Despejamos la componente Fy de la fuerza:
Fy = F·sen α
![]()
Despejamos la componente Fₓ de la fuerza:
Fₓ = F·cos α
De la ecuación (2) despejamos "N":
N = -Fy + P
Reemplazamos:
N = -F·sen α + P (3)
También reemplazamos en la ecuación (1):
Fₓ - Fᵣ = 0
F·cos α - μₑ·N = 0
Despejamos "N":
![]() (4)
(4)
Igualamos (3) y (4):
![]()
Despejamos "F":
(-F·sen α + P)·μₑ = F·cos α
-F·μₑ·sen α + P·μₑ = F·cos α
-F·μₑ·sen α - F·cos α = -P·μₑ
F·μₑ·sen α + F·cos α = P·μₑ
F·(μₑ·sen α + cos α) = P·μₑ
![]()
Reemplazamos por los datos y calculamos:

Resultado, la fuerza mínima para poner la caja en movimiento con α = 30° es:
F = 102,91 N
b)
Para α = 0°:
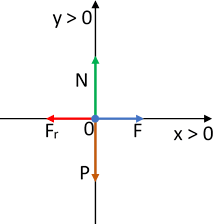
Diagrama de fuerzas
En el eje X:
F - Fᵣ = 0 (1)
En el eje Y:
N - P = 0 (2)
Reemplazamos Fᵣ en la ecuación (1):
F - μₑ·N = 0 (3)
Despejamos "N" de la ecuación (2):
N = P
Reemplazamos P por N en la ecuación (3):
F - μₑ·P = 0
Despejamos F:
F = μₑ·P
Reemplazamos por los datos y calculamos:
F = 0,6·200 N
Resultado, la fuerza mínima para poner la caja en movimiento con α = 0° es:
F = 120 N
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP03
- | Siguiente ›
Ejemplo, cómo calcular la fuerza resultante de un sistema de masas en movimiento