Problema nº 2 de dinámica con rozamiento, fuerza resultante de un sistema en un plano inclinado - TP03
Enunciado del ejercicio nº 2
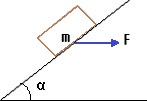
Calcular la fuerza máxima en la dirección de la base del plano que hay que ejercer, para que el cuerpo no se mueva, así como la fuerza mínima.
Desarrollo
Datos:
μ = 0,3
m = 5 kg
α = 30°
Se adopta g = 10 m/s²
Fórmulas:
P = m·g (1)
F = m·a (2)
Fᵣ = μ·N (3)
Condición de equilibrio (Primera ley de Newton):
∑Fₓ = 0
∑Fy = 0
∑MF = 0
Esquema:
Solución
La fuerza de rozamiento siempre es contraria al movimiento y, por lo tanto, actúa como freno.
En el primer caso (a) consideraremos a la fuerza de rozamiento con sentido al eje de las "X", lo que nos dará el valor mínimo de la fuerza F necesario para subir el bloque. En el segundo caso (b) orientaremos a la fuerza de rozamiento en el sentido de las "x > 0", lo que nos dará el valor mínimo de la fuerza "F" para evitar que el bloque se deslice hacia abajo.
a)
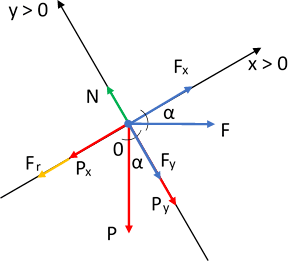
Diagrama de fuerzas
En el eje X:
Fₓ - Pₓ - Fᵣ = 0 (4)
En el eje Y:
N - Fy - Py = 0 (5)
También sabemos que:
![]()
Despejamos la componente Fy de la fuerza:
Fy = F·sen α
![]()
Despejamos la componente Fₓ de la fuerza:
Fₓ = F·cos α
Y que:
![]()
Despejamos la componente Pₓ de la fuerza peso:
Pₓ = P·sen α
![]()
Despejamos la componente Py de la fuerza peso:
Py = P·cos α
En las ecuaciones (4) y (5) reemplazamos las componentes:
F·cos α - P·sen α - Fᵣ = 0
N - F·sen α - P·cos α = 0
Luego reemplazamos "P" y "Fᵣ" por las fórmulas (2) y (3):
F·cos α - m·g·sen α - μ·N = 0 (6)
N - F·sen α - m·g·cos α = 0 (7)
De la ecuación (7) despejamos "N":
N = F·sen α + m·g·cos α
Y reemplazamos "N" en la (6):
F·cos α - m·g·sen α - μ·(F·sen α + m·g·cos α) = 0
Realizamos las operaciones algebraicas necesarias para despejar "F":
F·cos α - m·g·sen α - μ·F·sen α - μ·m·g·cos α = 0
F·cos α - μ·F·sen α = m·g·sen α + μ·m·g·cos α
F·(cos α - μ·sen α) = m·g·(sen α + μ·cos α)
![]()
Reemplazamos por los datos y calculamos:

Resultado, la fuerza mínima para poner al bloque en movimiento es:
F = 53,1 N
b)
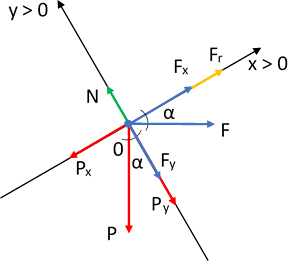
Diagrama de fuerzas
En el eje X:
Fₓ - Pₓ + Fᵣ = 0 (4)
En el eje Y:
N - Fy - Py = 0 (5)
También sabemos que:
![]()
Despejamos la componente Fy de la fuerza:
Fy = F·sen α
![]()
Despejamos la componente Fₓ de la fuerza:
Fₓ = F·cos α
Y que:
![]()
Despejamos la componente Pₓ de la fuerza peso:
Pₓ = P·sen α
![]()
Despejamos la componente Py de la fuerza peso:
Py = P·cos α
En las ecuaciones (4) y (5) reemplazamos las componentes:
F·cos α - P·sen α + Fᵣ = 0
N - F·sen α - P·cos α = 0
Luego reemplazamos "P" y "Fᵣ" por las fórmulas (2) y (3):
F·cos α - m·g·sen α + μ·N = 0 (6)
N - F·sen α - m·g·cos α = 0 (7)
De la ecuación (7) despejamos "N":
N = F·sen α + m·g·cos α
Y reemplazamos "N" en la (6):
F·cos α - m·g·sen α + μ·(F·sen α + m·g·cos α) = 0
Realizamos las operaciones algebraicas necesarias para despejar "F":
F·cos α - m·g·sen α + μ·F·sen α + μ·m·g·cos α = 0
F·cos α + μ·F·sen α = m·g·sen α - μ·m·g·cos α
F·(cos α + μ·sen α) = m·g·(sen α - μ·cos α)
![]()
Reemplazamos por los datos y calculamos:

Resultado, la fuerza mínima para evitar que el bloque se deslice es:
F = 11,8 N
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP03
- | Siguiente ›
Ejemplo, cómo calcular la fuerza resultante de un sistema en un plano inclinado