Problema nº 10 de dinámica, velocidad final en un plano inclinado - TP03
Enunciado del ejercicio nº 10
Calcular la velocidad que tiene el bloque al llegar a la base de un plano inclinado de α = 30°, α = 45°, α = 20°; si parte del reposo desde una altura h = 10 m.
Desarrollo
Datos:
v₁ = 0
h = 10 m
g = 9,80665 m/s²
Fórmulas:
Condición de equilibrio (Primera ley de Newton):
∑Fₓ = 0
∑Fy = 0
∑MF = 0
v₂² - v₁² = 2·a·d
Esquema:
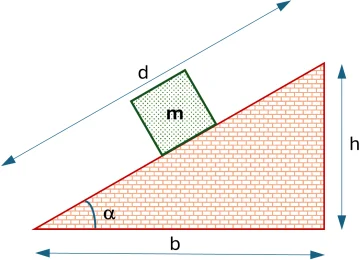
Solución
Descomponemos la fuerza peso en el eje de coordenadas:
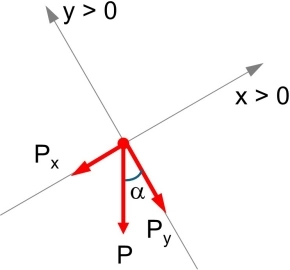
Diagrama de fuerzas
En el eje X hay movimiento:
∑Fₓ = m·a
Pₓ = m·a (1)
En el eje Y no hay movimiento:
∑Fy = 0
N - Py = 0 (2)
Por trigonometría sabemos que:
| sen α = | Pₓ |
| P |
Pₓ = P·sen α
| sen α = | h |
| d |
| d = | h | (3) |
| sen α |
Para hallar la velocidad debemos conocer la aceleración y la distancia recorrida, por tanto, la ecuación (1) queda:
m·a = P·sen α
m·a = m·g·sen α
Cancelamos la masa m:
a = g·sen α (4)
Reemplazamos en la ecuación combinada de cinemática:
v₂² - v₁² = 2·a·d
v₁ = 0
v₂² = 2·a·d
| v₂² = 2·g·sen α· | h |
| sen α |
Simplificamos:
v₂² = 2·g·h
La velocidad final no depende de la aceleración ni del ángulo.
Reemplazamos por los valores y calculamos:
v₂² = 2·9,80665 m/s²·10 m
v₂² = 196,133 m²/s²
v₂ = √196,133 m²/s²
v₂ = 14,00474919 m/s
Resultado, la velocidad que tiene el bloque al llegar a la base es:
v₂ = 14 m/s
Nota: En el plano inclinado, sin fuerzas de rozamiento ni fuerzas aplicadas, la velocidad no depende de la inclinación.
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP03
- | Siguiente ›
Ejemplo, cómo calcular la velocidad de un cuerpo en un plano inclinado.