Problema nº 2 de dinámica, fuerza de un cuerpo en movimiento y tiempo de frenado - TP04
Enunciado del ejercicio nº 2
A un cuerpo de 10 kg de masa se mueve con una velocidad constante de 5 m/s sobre una superficie horizontal. El coeficiente cinético de rozamiento entre el cuerpo y la superficie es de 0,2. Determinar:
a) ¿Qué fuerza horizontal se necesita para mantener el movimiento?
b) Si se suprime la fuerza, ¿cuándo se detendrá el cuerpo?
Desarrollo
Datos:
m = 10 kg
v = 5 m/s
μ = 0,2
v₂ = 0
g = 10 m/s²
Fórmulas:
P = m·g
Fᵣ = μ·P
F = m·a
v₂ = v₁ + a·t
Esquema:
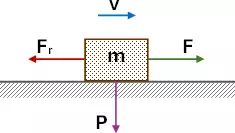
Solución
a)
La sumatoria de las fuerzas en X debe ser cero porque el cuerpo se mueve con velocidad constante (no hay aceleración).
F - Fᵣ = 0
Despejamos F:
F = Fᵣ
F = μ·P
F = μ·m·g
Reemplazamos por los datos y calculamos:
F = 0,2·10 kg·10 m/s²
F = 20 N
Resultado a), la fuerza horizontal es:
F = 20 N
b)
Para hallar el tiempo debemos conocer la desaceleración del sistema en el instante que deja de aplicarse la fuerza:
F = m·a
![]()
![]()
a = 2 m/s²
Luego aplicamos la ecuación horaria de la velocidad:
v₂ = v₁ + a·t
La velocidad final será nula.
0 = v₁ + a·t
v₁ = -a·t
Despejamos el tiempo t:
![]()
a < 0 ⇒ desaceleración
![]()
t = 2,5 s
Resultado b), el tiempo que demora en detenerse es:
t = 2,5 s
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP04
- | Siguiente ›
Ejemplo, cómo calcular la aceleración de un cuerpo en movimiento.