Problema nº 3 de dinámica, fuerza de un cuerpo en movimiento y tiempo de frenado - TP04
Enunciado del ejercicio nº 3
Una bala de rifle que lleva una velocidad de 360 m/s, choca contra un bloque de madera blanda y penetra con una profundidad de 0,1 m. La masa de la bala es de 1,8 g, suponiendo una fuerza de retardo constante, determinar:
a) ¿Qué tiempo tardó la bala en detenerse?
b) ¿Cuál fue la fuerza de aceleración en N?
Desarrollo
Datos:
v₁ = 360 m/s
Δx = 0,1 m
m = 1,8 g
Fórmulas:
v₂² - v₁² = 2·a·Δx (1)
v₂ - v₁ = a·t (2)
F = m·a (3)
Solución
a)
Para obtener el tiempo que demora en detenerse primero debemos hallar la aceleración.
De la ecuación (1):
v₂² - v₁² = 2·a·Δx
v₂ = 0 m/s
v₁² = 2·a·Δx
Despejamos a:
![]()
Reemplazamos por los datos y calculamos:

a = -648.000 m/s² (a < 0 ⇒ desaceleración)
De la ecuación (2):
v₂ - v₁ = a·t
v₂ = 0 m/s
-v₁ = a·t
Despejamos t:
![]()
Reemplazamos por los datos y calculamos:
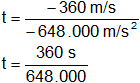
t = 0,000555556 s
Resultado a), el tiempo que tardó la bala en detenerse es:
t = 5,56·10⁻⁴ s
b)
Con los datos dados y obtenidos aplicamos la ecuación (3):
F = a·m
Convertimos las unidades:
![]()
m = 0,0018 kg
Reemplazamos por los datos y calculamos:
F = -648.000 m/s²·0,0018 kg
F = -1.166,4 kg·m/s²
Resultado b), la fuerza de aceleración es:
F = -1.166,4 N
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP04
- | Siguiente ›
Ejemplo, cómo calcular la desaceleración de un cuerpo en movimiento.