Problema nº 7 de dinámica, fuerza y aceleración de cuerpos en movimiento - TP04

Enunciado del ejercicio nº 7

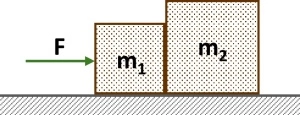
Calcular el valor de m₁ y el de m₂ para el sistema de la figura, sabiendo que suman 12 kg y que cuando se aplica una fuerza F = 30 kgf, el bloque 1 le transmite al bloque 2 una fuerza F₁₂ = 20 kgf.

Desarrollo

Datos:

mₜ = 12 kg

F = 30 kgf

F₁₂ = 20 kgf

Fórmulas:

F = m·a

Condición de equilibrio (Primera ley de Newton):

∑F = 0

Solución

Condición de equilibrio:

∑F = 0

Hay movimiento, por tanto:

∑F = m·a

Planteamos la sumatoria de las fuerzas para el sistema:

F + F₁₂ - F₂₁ = mₜ·a

F₁₂ = F₂₁

F = mₜ·a (1)

Donde,

mₜ = m₁ + m₂ = 12 kg (2)

Luego:

F₁₂ = m₂·a

Despejamos la aceleración a:

Reemplazamos la aceleración en la ecuación (1):

Despejamos m₂:

Reemplazando por los datos y calculamos:

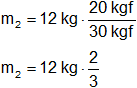
m₂ = 8 kg

Resultado a), la masa 2 es:

m₂ = 8 kg

Con este valor, reemplazamos en la ecuación (2):

m₁ + m₂ = 12 kg

m₁ + 8 kg = 12 kg

Despejamos m₁:

m₁ = -8 kg + 12 kg

m₁ = 4 kg

Resultado b), la masa 1 es:

m₁ = 4 kg

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP04
• | Siguiente ›

Ejemplo, cómo calcular la aceleración y la fuerza de cuerpos en movimiento.