Problema nº 3 de dinámica, cuerpos sometidos a fuerzas, aceleración y tensión con plano inclinado - TP05

Enunciado del ejercicio nº 3

Calcular para el sistema de la figura su aceleración y la tensión en la cuerda si m₁ = 12 kg, m₂ = 8 kg y α = 30°.

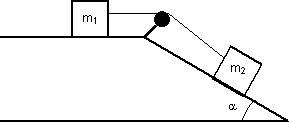
Esquema de los cuerpos y la fuerza en un plano inclinado

Desarrollo

Datos:

m₁ = 12 kg

m₂ = 8 kg

α = 30°

Se adopta g = 10 m/s²

Fórmulas:

Condición de equilibrio (Primera ley de Newton):

∑F = 0

F = m·a

P = m·g

Solución

Los gráficos correspondientes a las masas puntuales son:

Diagrama del cuerpo libre de la masa 1

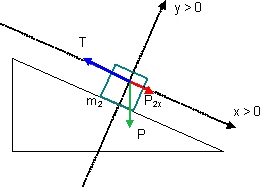
Diagrama del cuerpo libre de la masa 2 en el plano inclinado

Nos interesa particularmente el movimiento a lo largo del eje X, la condición de equilibrio es:

∑Fₓ = 0

Pero como hay movimiento:

∑Fₓ = m·a

La ecuación en el eje X es:

P₂ₓ - T = m₂·a

T = P₂·sen 30° - m₂·a (para la masa 2)

T = m₁·a (para la masa 1)

Igualando:

m₁·a = P₂·sen 30° - m₂·a

m₁·a + m₂·a = P₂·sen 30°

(m₁ + m₂)·a = P₂·sen 30°

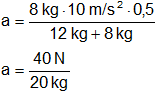
Resultado 1:

a = 2 m/s²

Luego:

T = m₁·a

T = 12 kg·2 m/s²

Resultado 2:

T = 24 N

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP05
• | Siguiente ›

Ejemplo de cuerpos sometidos a fuerzas, como calcular la aceleración y la tensión con plano inclinado.