Problema nº 4 de dinámica, aceleración, tiempo y fuerza de un electrón. - TP07
Enunciado del ejercicio nº 4
Un electrón (masa = 9·10⁻³¹ kg) sale del cátodo de una lámpara de radio partiendo del reposo y viaja en línea recta hasta el ánodo, que está a 0,01 m de distancia, y llega con una velocidad de 6·10⁶ m/s. Si la fuerza que lo acelera es constante (despreciar la fuerza gravitatoria sobre el electrón), calcular:
a) La fuerza de aceleración.
b) El tiempo que empleó en llegar al ánodo.
c) La aceleración.
Desarrollo
Datos:
m = 9·10⁻³¹ kg
Δx = 0,01 m
v₁ = 0
v₂ = 6·10⁶ m/s
Fórmulas:
v₂² = v₁² + 2·a·Δx (1)
F = m·a (2)
v₂ - v₁ = a·t (3)
Solución
No respetamos el orden de cálculos.
c)
Primero hallamos la aceleración del sistema, aplicamos la ecuación combinada de cinemática:
v₂² - v₁² = 2·a·Δx
Despejamos a de la ecuación (1):
![]()
Reemplazamos con los datos y calculamos:
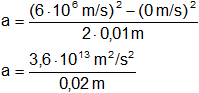
a = 1,8·10¹⁵ m/s²
Resultado c), la aceleración del electrón es:
a = 1,8·10¹⁵ m/s²
a)
Con el dato de la aceleración podemos calcular la fuerza aplicada al sistema.
Aplicamos la ecuación (2):
F = m·a
Reemplazamos con los datos y calculamos:
F = 9·10⁻³¹ kg·1,8·10¹⁵ m/s²
F = 1,62·10⁻¹⁵ N
Resultado a), la fuerza del sistema es:
F = 1,62·10⁻¹⁵ N
c)
Para calcular el tiempo aplicamos la ecuación (3):
v₂ - v₁ = a·t
Despejamos t:
![]()
Reemplazamos por los datos y calculamos:

t = 3,33·10⁻⁹ s
Resultado b), el tiempo que empleó en llegar al ánodo es:
t = 3,33·10⁻⁹ s
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP07
- | Siguiente ›
Ejemplo, cómo calcular la aceleración, el tiempo y la fuerza de un electrón.