Problema nº 1 de dinámica, tensiones de cuerdas en un movimiento por etapas - TP08

Enunciado del ejercicio nº 1

Un bloque de 5 kg de masa está sostenido por una cuerda que tira de él hacia arriba con una aceleración de 2 m/s²

a) ¿Cuál es la tensión de la cuerda?

b) Después de haberse puesto en movimiento el bloque, la tensión de la cuerda disminuye a 49 N. ¿Qué clase de movimiento tendrá entonces el bloque?

c) Si se afloja completamente la cuerda, se observa que el bloque asciende aún 2 m antes de detenerse. ¿Qué velocidad llevaba cuando se aflojó la cuerda?

Desarrollo

Datos:

m = 5 kg

aᵣ = 2 m/s²

T₂ = 49 N

h = 2 m

g = 9,8 m/s²

Fórmulas:

P = m·g

Condición de equilibrio (Primera ley de Newton):

∑Fₓ = 0

∑F_y = 0

∑MF = 0

Esquema:

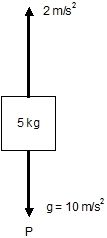
Diagrama del cuerpo libre

Solución

P = m·g

P = 5 kg·9,8 m/s²

P = 49 N

La tensión de la cuerda es:

T - P = m·aᵣ

m·a - m·g = m·aᵣ

a - g = aᵣ

a = g + aᵣ

a = 9,8 m/s² + 2 m/s²

a = 11,8 m/s²

T = m·a

T = 5 kg·11,8 m/s²

Resultado, la tensión de la cuerda es:

T = 59 N

Cuando la tensión disminuye:

T - P = Fᵣ

Fᵣ = 49 N - 49 N

Fᵣ = 0 N

Resultado, las fuerzas están en equilibrio, significa que no hay movimiento, por lo tanto, es un MRU.

Hallando la velocidad del bloque en el momento en que la tensión cesa, siendo la velocidad final nula y la aceleración de frenado es la aceleración de la gravedad:

V_f² - Vᵢ² = 2·aᵣ·h

0 - Vᵢ² = 2·(-9,8 m/s²)·2 m

-Vᵢ² = -39,2 m²/s²

Vᵢ² = 39,2 m²/s²

Vᵢ = √39,2 m²/s²

Resultado, la velocidad del bloque cuando se aflojó la cuerda es:

Vᵢ = 6,261 m/s

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular tensiones de cuerdas en un movimiento por etapas.