Problema nº 3 de dinámica, fuerza de rozamiento de un cuerpo en movimiento y tiempo - TP08
Enunciado del ejercicio nº 3
Una caja de 15 kg de masa descansa sobre la plataforma de un camión. El coeficiente de rozamiento entre la caja y el suelo es de 0,1. El camión inicia su marcha con una aceleración de 1,5 m/s². Si la caja se encuentra a 4 m del final del camión cuando éste arranca, determinar:
a) ¿Cuánto tiempo transcurrirá hasta que la caja salga despedida del camión por su parte trasera?
b) ¿Qué distancia recorrerá el camión en ese tiempo?
Desarrollo
Datos:
m = 15 kg
ac = 1,5 m/s²
μ = 0,1
Δx = 4 m
vᵢ = 0
g = 10 m/s²
Fórmulas:
P = m·g
Fᵣ = μ·N
F = m·ac
Δx = v₀·t + ½·a·t²
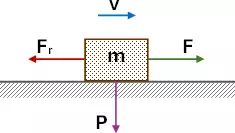
Esquema:
Solución
a)
Para determinar el tiempo necesitamos la aceleración del sistema.
F: es la fuerza que el camión ejerce sobre el bulto.
En el momento que el camión arranca la sumatoria de las fuerzas en X es igual a m·a del sistema, hay aceleración.
F - Fᵣ = m·aₛ (1)
La reacción del vínculo es N, pero:
N = P
Fᵣ = μ·P
Fᵣ = μ·m·g
Luego, de (1):
m·ac - μ·m·g = m·aₛ
Cancelamos m que es la masa del bulto:
ac - μ·g = aₛ
Reemplazamos y calculamos:
aₛ = 1,5 m/s² - 0,1·10 m/s²
aₛ = 1,5 m/s² - 1 m/s²
aₛ = 0,5 m/s²
Con la aceleración del sistema calculamos el tiempo aplicando la ecuación horaria de posición:
Δx = v₀·t + ½·aₛ·t²
vᵢ = 0
Entonces:
Δx = ½·aₛ·t²
Despejamos t:
| t² = | 2·Δx |
| aₛ |
Reemplazamos y calculamos:
| t² = | 2·4 m |
| 0,5 m/s² |
| t² = | 8 s² |
| 0,5 |
t² = 16 s²
t = √16 s²
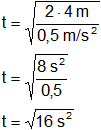
t = 4 s
Resultado a), el tiempo transcurrido hasta que el bulto sale despedido es:
t = 4 s
b)
Aplicamos nuevamente la ecuación horaria de posición pero con la aceleración del camión ac:
Δx = v₀·t + ½·ac·t²
vᵢ = 0
Entonces:
Δx = ½·ac·t²
Reemplazamos y calculamos:
Δx = ½·1,5 m/s²·(4 s)²
Δx = 0,75 m/s²·16 s²
Δx = 12 m
Resultado b), la distancia que recorre el camión en ese tiempo es:
Δx = 12 m
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP08
- | Siguiente ›
Ejemplo, cómo calcular el tiempo y la distancia