Problema nº 9 de dinámica, aceleración y fuerza en un sistema de masas en movimiento - TP08

Enunciado del ejercicio nº 9

Si en el problema anterior, el estiramiento del resorte es de 60 cm cuando el sistema se acelera, calcular su aceleración y la fuerza F.

Desarrollo

Datos:

m₁ = 40 kg

m₂ = 20 kg

k = 30 N/m

x = 60 cm

Fórmulas:

P = m·g

F = k·x

∑F = m·a

Esquema:

Solución

Realizamos los gráficos correspondientes a las masas puntuales.

Cuerpo 1:

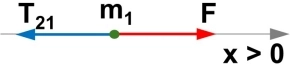
Cuerpo 2:

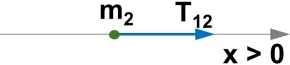
Seleccionamos el sentido del eje de coordenadas más conveniente.

Aplicamos la condición de equilibrio de las fuerzas en movimiento:

∑F = m·a

F - T₂₁ = m₁·a (1)

T₁₂ = m₂·a (2)

T₂₁ = T₁₂ = T

Las ecuaciones (1) y (2) quedan:

F - T = m₁·a (1)

T = m₂·a (2)

Aplicamos la fórmula dada para hallar T empleando la ecuación (2):

T = k·x

k·x = m₂·a

Despejamos el estiramiento del resorte a:

Adecuamos las unidades:

x = 0,6 m

Reemplazamos por los valores y calculamos:

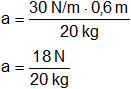
a = 0,9 m/s²

Resultado a), la aceleración del sistema es:

a = 0,9 m/s²

Para calcular la fuerza F sumamos las ecuaciones (1) y (2) miembro a miembro:

F = m₁·a + m₂·a

Reemplazamos por los valores y calculamos:

F = 40 kg·0,9 m/s² + 20 kg·0,9 m/s²

F = 36 kg·m/s² + 18 kg·m/s²

F = 54 N

Resultado b), el valor de la fuerza F es:

F = 54 N

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP08
• | Siguiente ›

Ejemplo, cómo calcular la fuerza y la aceleración en un sistema de masas en movimiento.