Problema nº 4 de dinámica, fuerza de frenado aplicada a un cuerpo en movimiento - TP09
Enunciado del ejercicio nº 4
¿Cuál es la fuerza capaz de detener completamente a un automóvil de 2.000 kg de masa en 80 metros, cuando este lleva una velocidad de 72 km/h?
Desarrollo
Datos:
m = 2.000 kg
v₁ = 72 km/h
Δx = 80 m
Fórmulas:
v₂² - v₁² = 2·a·Δx
F = m·a
Solución
Empleamos la ecuación combinada de velocidad para hallar la aceleración:
v₂² - v₁² = 2·a·Δx
El móvil se detiene, por tanto:
v₂ = 0
-v₁² = 2·a·Δx
Despejamos a:
| a = | -v₁² |
| 2·Δx |
Adecuamos las unidades:
| v₁ = 72 km/h· | 1 h | · | 1.000 m |
| 3.600 s | 1 km |
v₁ = 20 m/s
Reemplazamos y calculamos:
| a = | -(20 m/s)² |
| 2·80 m |
| a = | -400 m²/s² |
| 160 m |
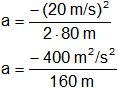
a = -2,5 m/s²
La aceleración es negativa porque se trata de detener al móvil.
Reemplazamos en la fórmula de la fuerza en función de la masa y la aceleración
F = m·a
Reemplazamos y calculamos:
F = 2.000 kg·(-2,5 m/s²)
F = -5.000 N
Resultado, la fuerza necesaria para detener al automóvil es:
F = -5.000 N
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP09
- | Siguiente ›
Ejemplo, cómo calcular la fuerza de frenado de un cuerpo en movimiento.