Elasticidad en los sólidos, líquidos y gases I
Elasticidad en los sólidos
Los sólidos reales no son cuerpos rígidos, pues se deforman por la acción de fuerzas exteriores. Las deformaciones originan reacciones internas, llamadas fuerzas elásticas, que equilibran a las fuerzas aplicadas.
Nos referiremos a la elasticidad en sólidos isótropos y homogéneos. Son homogéneos los cuerpos cuyas propiedades son las mismas en todos sus puntos, y son isótropos cuando en cada punto las propiedades físicas son idénticas en todas las direcciones.
Elasticidad por tracción
Colocando una carga P en el extremo B de un alambre fijo en su otro extremo A se observa un alargamiento Δl.
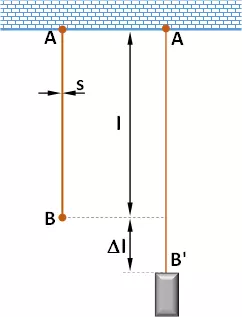
Siendo l la longitud inicial y s el área de la sección normal del alambre, se comprueba que el alargamiento Δl cumple, para cargas que no pasan de cierto límite, las siguientes leyes:
1) Es proporcional a la carga P (fuerza peso).
2) Es proporcional a la longitud l.
3) Es inversamente proporcional a la sección s.
4) El factor de proporcionalidad es un coeficiente K, que depende de la sustancia de que está hecho el alambre.
Puede, pues, escribirse:
| Δl = K· | P·l |
| s |
Recordemos que el peso P es una fuerza, para este concepto, el alargamiento puede ser producido por el peso o por una fuerza F, y que, la presión (p) es:
| p = | P | = | F |
| s | s |
El coeficiente K, llamado coeficiente de elasticidad por tracción, se suele expresar en la forma:
| K = | 1 |
| E |
Siendo E el módulo de elasticidad por tracción (módulo de Young). Reemplazamos en la primera fórmula:
| Δl = | F·l |
| E·s |
Si aumentamos la carga F (P en el esquema), se llegará a un valor a partir del cual los alargamientos dejan de ser proporcionales a las cargas. Se ha pasado, pues, el límite de proporcionalidad. Hasta este límite, se puede admitir con suficiente aproximación que, retirada la carga, el alambre recobrará su longitud inicial.
De la fórmula anterior deducimos:
| F | = | E·Δl |
| s | l |
El cociente F/s = σ es la fuerza que actúa por unidad de la superficie de la sección del alambre, se mide en unidades de presión (Pa) o tensión y, se la llama tensión.
| σ = | F | ⟶ [p] = | N | ; | N | = Pa |
| s | mm² | m² |
La relación Δl/l = ε es el alargamiento experimentado por unidad de longitud, o sea la deformación, es adimensional.
| ε = | Δl | = | l - l₀ |
| l | l₀ |
Luego, la fórmula:
Luego, la fórmula:
| F | = | E·Δl |
| s | l |
Puede escribirse:
σ = ε·E
Que dice: las tensiones son proporcionales a las deformaciones (ley de Hook).
Siendo ε un número abstracto, pues es el cociente de dos longitudes, la unidad en que se mide E será la misma en que se mide σ, o sea:
[E] = Pa
Otra expresión del módulo de Young es:
| E = | F·l |
| s·Δl |
Bibliografía:
"Física elemental". José S. Fernández y Ernesto E. Galloni. Argentina.
"Física Universitaria". Sears, Zemansky, Young. España.
Autor: Ricardo Santiago Netto. Argentina