Elasticidad en los sólidos, líquidos y gases VI
Deslizamiento
Imaginemos un paralelepípedo ABCDEIGH y sobre dos caras opuestas ABIE y CDGH aplicadas fuerzas F y -F uniformemente repartidas en dirección tangencia a las mismas. Se producirá una deformación tal, que el volumen se mantiene constante, pero se modifican los ángulos diedros, cuyas aristas son perpendiculares al plano determinado por F y -F.
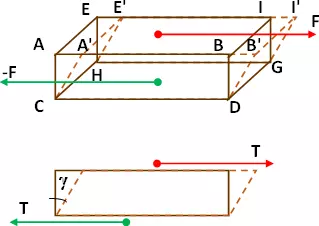
Decimos que se ha producido un deslizamiento que mediremos por el ángulo γ.
Si llamamos T a la tensión tangencial que produce el deslizamiento, se verifica que:
![]()
T = G·λ
Fórmula análoga a:
σ = ε·E
Pues indica que la tensión es proporcional a la deformación. El coeficiente G se llama módulo de elasticidad por deslizamiento, o módulo de rigidez, o módulo de torsión y es constante para cada material.
Su valor es del orden de 0,4·E (ver tabla de constantes de elasticidad de metales).
Bibliografía:
"Física elemental". José S. Fernández y Ernesto E. Galloni. Argentina.
"Física Universitaria". Sears, Zemansky, Young. España.
Autor: Ricardo Santiago Netto. Argentina